题目内容
已知正方体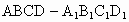 中,E、F分别为
中,E、F分别为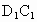 、
、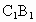 的中点,
的中点,
AC∩BD=P,
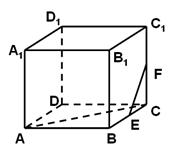
求证:(1)D、B、F、E四点共面;
(2)若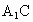 交平面DBFE于R点,则P、Q、R三点共线.
交平面DBFE于R点,则P、Q、R三点共线.
答案:略
解析:
提示:
解析:
|
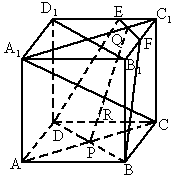
证明:如图, (1)∵EF是 的中位线,∴ 的中位线,∴ . .
在正方体 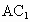 中, 中, ,∴EF∥BD. ,∴EF∥BD.
∴ EF,BD确定一个平面,即D、B、F、E四点共面.(2) 正方体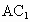 中,设 中,设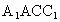 确定的平面为a
,又设平面BDEF为b 确定的平面为a
,又设平面BDEF为b
∵  , ,
∴ QÎ a ,又QÎ EF,∴ QÎ b则 Q是a 与b 的公共点,同理, P点也是a 与b 的公共点,∴a ∩b =PQ又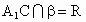
∴  , ,
∴ RÎ a ,且RÎ b ,则 RÎ PQ故P、Q、R在点共线. |
提示:
|
证明共面问题利用公理2,证明三点共线或三线共点,利用公理3. |

练习册系列答案
 新课标快乐提优暑假作业陕西旅游出版社系列答案
新课标快乐提优暑假作业陕西旅游出版社系列答案
相关题目
 中,E、F分别为
中,E、F分别为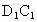 、
、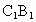 的中点,
的中点,
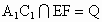
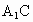 交平面DBFE于R点,则P、Q、R三点共线.
交平面DBFE于R点,则P、Q、R三点共线.
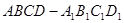 中,E、F分别为棱BC和
中,E、F分别为棱BC和
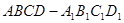 中,E、F分别为棱BC和
中,E、F分别为棱BC和