题目内容
设函数y=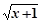 的定义域为M,集合N={y|y=x2,x∈R},则M∩N= ( )
的定义域为M,集合N={y|y=x2,x∈R},则M∩N= ( )
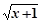 的定义域为M,集合N={y|y=x2,x∈R},则M∩N= ( )
的定义域为M,集合N={y|y=x2,x∈R},则M∩N= ( )A.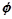 | B.N | C.[1,+∞) | D.M |
B
分析:根据负数没有平方根列出不等式,求出不等式的解集确定出函数的定义域M;根据完全平方式恒大于等于0,得到二次函数的值域确定出集合N,然后求出两集合的交集即可.
解答:解:根据题意得:x+1≥0,解得x≥-1,
∴函数的定义域M={x|x≥-1};
∵集合N中的函数y=x2≥0,
∴集合N={y|y≥0},
则M∩N={y|y≥0}=N.
故选B
解答:解:根据题意得:x+1≥0,解得x≥-1,
∴函数的定义域M={x|x≥-1};
∵集合N中的函数y=x2≥0,
∴集合N={y|y≥0},
则M∩N={y|y≥0}=N.
故选B

练习册系列答案
相关题目
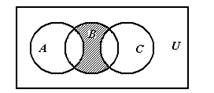
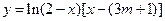 的定义域为集合A,集合 B={
的定义域为集合A,集合 B={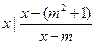 <0}.
<0}.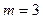 时,求A
时,求A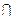 B;
B; 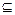 A的实数
A的实数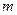 的取值范围。
的取值范围。
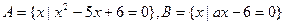 ,且
,且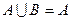 ,
,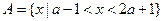 ,
,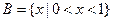 ,若
,若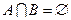 ,求实数a的取值范围。
,求实数a的取值范围。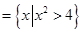 ,N
,N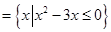 ,则
,则 (▲)
(▲)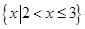 B.
B.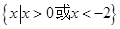
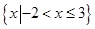 D.
D.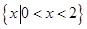
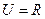 ,
,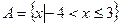 ,
,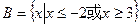 ,求:
,求: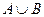 ; (2)
; (2)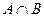 ; (3)
; (3)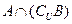
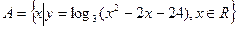 ,
,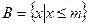 ,
,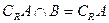 ,求实数m的取值范围.
,求实数m的取值范围.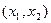 表示,其中
表示,其中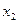 ,
,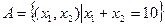 ,
,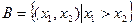 ,则
,则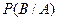 等于________________.
等于________________.