题目内容
已知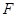 为双曲线
为双曲线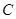 :
: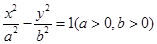 的右焦点,
的右焦点,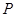 为双曲线
为双曲线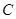 右支上一点,
右支上一点,
且位于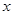 轴上方,
轴上方,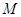 为直线
为直线 上一点,
上一点,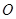 为坐标原点,已知
为坐标原点,已知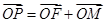 ,
,
且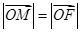 ,则双曲线
,则双曲线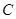 的离心率为
的离心率为
A.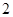 | B.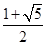 | C. | D.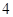 |
A
解析考点:双曲线的简单性质.
分析:先确定M的坐标,再确定P的坐标,代入双曲线方程,即可求得结论.
解:由题意,M位于x轴上方
∵|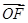 |=|
|=|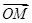 |,M为直线x=-
|,M为直线x=-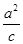 上一点
上一点
∴M(-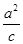 ,
,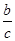
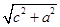 )
)
∵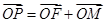
∴四边形OMPF为菱形
∴P(c-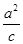 ,
,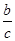
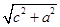 ),即P(
),即P(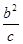 ,
,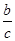
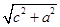 )
)
代入双曲线方程可得 -
- =1
=1
化简可得c2=4a2
∴c=2a,
∴e=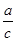 =2
=2
故选A.

练习册系列答案
 亮点激活精编提优100分大试卷系列答案
亮点激活精编提优100分大试卷系列答案
相关题目
已知双曲线 ,则p的值为( )
,则p的值为( )
| A.-2 | B.-4 | C.2 | D.4 |
设A是椭圆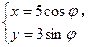 (
(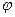 是参数)的左焦点,P是椭圆上对应于
是参数)的左焦点,P是椭圆上对应于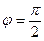 的点,那么线段AP的长是
的点,那么线段AP的长是
| A.1 | B.5 | C.7 | D.10 |
已知抛物线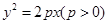 ,过点
,过点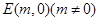 的直线交抛物线于点M、N,交y轴于点P,若
的直线交抛物线于点M、N,交y轴于点P,若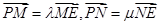 ,则
,则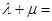 ( )
( )
| A.1 | B.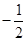 | C.-1 | D.-2 |
焦点为F(0,10),渐近线方程为4x±3y=0的双曲线的方程是 ( )
A.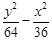 =1 =1 | B.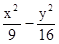 =1 =1 | C.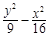 ="1" ="1" | D.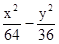 =1 =1 |
设双曲线C: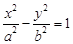 (a>0,b>0)的右焦点为F,左,右顶点分别为A1,A2.过F且与双曲线C的一条渐近线平行的直线l与另一条渐近线相交于P,若P恰好在以A1A2为直径的圆上,则双曲线C的离心率为
(a>0,b>0)的右焦点为F,左,右顶点分别为A1,A2.过F且与双曲线C的一条渐近线平行的直线l与另一条渐近线相交于P,若P恰好在以A1A2为直径的圆上,则双曲线C的离心率为
A.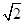 | B.2 | C. | D. 3 |
一条动圆圆心在抛物线上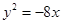 ,动圆恒过点(-2,0)则下列哪条直线是动圆的公切线()
,动圆恒过点(-2,0)则下列哪条直线是动圆的公切线()
| A.x=4 | B.y=4 | C.x=2 | D.x=-2 |
一抛物线形拱桥,当水面离桥顶2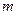 时,水面宽4
时,水面宽4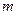 ,若水面下降1
,若水面下降1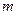 ,则水面宽为( )
,则水面宽为( )
A.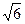  | B.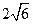  | C.4.5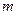 | D.9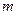 |
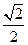 的动点的轨迹方程是 ( )
的动点的轨迹方程是 ( ) 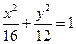 B.
B.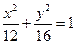 C
C 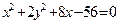 D.
D.