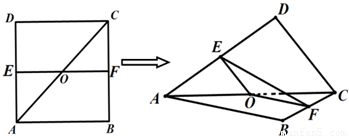
题目内容
 点O是边长为4的正方形ABCD的中心,点E,F分别是AD,BC的中点.沿对角线AC把正方形ABCD折成直二面角D-AC-B
点O是边长为4的正方形ABCD的中心,点E,F分别是AD,BC的中点.沿对角线AC把正方形ABCD折成直二面角D-AC-B
(1)求∠EOF的大小;
(2)求二面角E-OF-A的余弦值.
 解:(1)如图,过点E作EG⊥AC,垂足为G,过点F作FH⊥AC,垂足为H,则EG=FH=
解:(1)如图,过点E作EG⊥AC,垂足为G,过点F作FH⊥AC,垂足为H,则EG=FH= ,GH=2
,GH=2 .
.∵二面角D-AC-B为直二面角,∴EF2=GH2+EG2+FH2-2EG•FHcos90°=8+2+2-0=12
又在△EOF中,OE=OF=2,∴cos∠EOF=
 =
=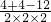 =-
=- .
. ∴∠EOF=120°.…..(6分)
(2)过点G作GM垂直于FO的延长线于点M,连EM.
∵二面角D-AC-B为直二面角,∴平面DAC⊥平面BAC,交线为AC,
又∵EG⊥AC,∴EG⊥平面BAC.
∵GM⊥OF,由三垂线定理,得EM⊥OF.
∴∠EMG就是二面角E-OF-A的平面角.…..(9分)
在Rt△EGM中,∠EGM=90°,EG=
 ,GM=
,GM= OE=1,
OE=1,∴tan∠EMG=
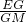 =
= ,∴cos∠EMG=
,∴cos∠EMG=
∴二面角E-OF-A的余弦值为
 .…..(12分)
.…..(12分)分析:(1)过点E作EG⊥AC,垂足为G,过点F作FH⊥AC,垂足为H,先求出EF,再利用余弦定理,即可求∠EOF的大小;
(2)过点G作GM垂直于FO的延长线于点M,连EM,证明∠EMG就是二面角E-OF-A的平面角,从而可求二面角E-OF-A的平面角.
点评:本题考查空间角,考查面面角,考查余弦定理的运用,考查学生的计算能力,属于中档题.

练习册系列答案
相关题目
 点O是边长为4的正方形ABCD的中心,点E,F分别是AD,BC的中点.沿对角线AC把正方形ABCD折成直二面角D-AC-B
点O是边长为4的正方形ABCD的中心,点E,F分别是AD,BC的中点.沿对角线AC把正方形ABCD折成直二面角D-AC-B