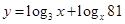题目内容
下列函数中,最小值是4的是( )
A、y=x+
| ||||||
B、y=2
| ||||||
| C、y=2(7x+7-x) | ||||||
D、y=sinx+
|
分析:利用基本不等式即可得出.
解答:解:A.当x<0时,y<0,故最小值不可能是4;
B.y=2
+
≥2
=4,但是等式不成立,因此最小值不可能是4;
C.y=2(7x+7-x)≥2×2
=4,当且仅当x=0时取等号,因此正确;
D.y=sinx+
,x∈[0,
],一是定义域存在问题,二利用基本不等式可得y>2
=4,最小值不可能是4.
综上可知:只有C正确.
故选:C.
B.y=2
| x2+2 |
| 2 | ||
|
2
|
C.y=2(7x+7-x)≥2×2
| 7x•7-x |
D.y=sinx+
| 4 |
| sinx |
| π |
| 2 |
sinx•
|
综上可知:只有C正确.
故选:C.
点评:本题考查了基本不等式的性质,使用时注意“一正二定三相等”的法则,使用基础题.

练习册系列答案
相关题目
 B.
B.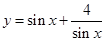 (
(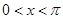 ) C.
) C.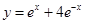 D.
D.