题目内容
 某加工厂用某原料由甲车间加工出A产品,由乙车间加工出B产品.甲车间加工一箱原料需耗费工时10小时,可加工出7千克A产品,每千克A产品获利40元.乙车间加工一箱原料需耗费工时6小时,可加工出4千克B产品,每千克B产品获利50元.甲、乙两车间每天共能完成至多70箱原料的加工,每天甲、乙车间耗费工时总和不得超过480小时,那么要满足上述的要求,并且获利最大,甲、乙两车间应当各生产多少箱?
某加工厂用某原料由甲车间加工出A产品,由乙车间加工出B产品.甲车间加工一箱原料需耗费工时10小时,可加工出7千克A产品,每千克A产品获利40元.乙车间加工一箱原料需耗费工时6小时,可加工出4千克B产品,每千克B产品获利50元.甲、乙两车间每天共能完成至多70箱原料的加工,每天甲、乙车间耗费工时总和不得超过480小时,那么要满足上述的要求,并且获利最大,甲、乙两车间应当各生产多少箱?
 解:设甲车间加工原料x箱,乙车间加工原料y箱,…(1分)
解:设甲车间加工原料x箱,乙车间加工原料y箱,…(1分)根据题意,得约束条件
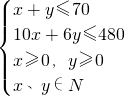 …(4分)
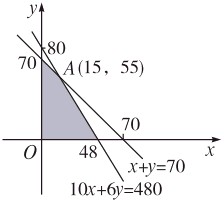
…(4分)画出可行域.…(7分)
目标函数z=280x+200y,…(8分)
即
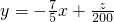 ,…(9分)
,…(9分)作直线
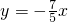 并平移,得直线经过点A(15,55)时z取最大值.…(11分)
并平移,得直线经过点A(15,55)时z取最大值.…(11分)所以当x=15,y=55时,z取最大值?.…(12分)
分析:根据已知条件,可得不等式组与目标函数,利用可行域,即可得到结论.
点评:本题考查线性规划知识的运用,考查数形结合的数学思想,考查学生的计算能力,属于中档题.

练习册系列答案
相关题目
某加工厂用某原料由甲车间加工出A产品,由乙车间加工出B产品.甲车间加工一箱原料需耗费工时10小时可加工出7千克A产品,每千克A产品获利40元.乙车间加工一箱原料需耗费工时6小时可加工出4千克B产品,每千克B产品获利50元.甲、乙两车间每天共能完成至多70多箱原料的加工,每天甲、乙车间耗费工时总和不得超过480小时,甲、乙两车间每天获利最大的生产计划为( )
| A、甲车间加工原料10箱,乙车间加工原料60箱 | B、甲车间加工原料15箱,乙车间加工原料55箱 | C、甲车间加工原料18箱,乙车间加工原料50箱 | D、甲车间加工原料40箱,乙车间加工原料30箱 |
 某加工厂用某原料由甲车间加工出A产品,由乙车间加工出B产品.甲车间加工一箱原料需耗费工时10小时,可加工出7千克A产品,每千克A产品获利40元.乙车间加工一箱原料需耗费工时6小时,可加工出4千克B产品,每千克B产品获利50元.甲、乙两车间每天共能完成至多70箱原料的加工,每天甲、乙车间耗费工时总和不得超过480小时,那么要满足上述的要求,并且获利最大,甲、乙两车间应当各生产多少箱?
某加工厂用某原料由甲车间加工出A产品,由乙车间加工出B产品.甲车间加工一箱原料需耗费工时10小时,可加工出7千克A产品,每千克A产品获利40元.乙车间加工一箱原料需耗费工时6小时,可加工出4千克B产品,每千克B产品获利50元.甲、乙两车间每天共能完成至多70箱原料的加工,每天甲、乙车间耗费工时总和不得超过480小时,那么要满足上述的要求,并且获利最大,甲、乙两车间应当各生产多少箱?