题目内容
己知函数f(x)=
,那么f(1)+f(2)+f(3)+…+f(2009)+f(
)+f(
)+…+f(
)=( )
| x2 |
| 1+x2 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 2009 |
分析:题目中给出了函数解析式,当然可以逐项求解,再相加.审题后,应当注意到所给的自变量的取值有特点:倒数关系,由此应先考虑f(x)+f(
)的结果的特殊性,以期减少重复的运算.
| 1 |
| x |
解答:解:∵f(x)=
,∴f(x)+f(
)=
+
=
+
=1
∴f(1)+f(2)+f(3)+…+f(2009)+f(
)+f(
)+…+f(
)
=f(1)+[f(2)+f(
)]+f(3)+f(
)]+…+[f(2009)+f(
)]
=
+1+1+…+1
=2008
故选:D.
| x2 |
| 1+x2 |
| 1 |
| x |
| x2 |
| 1+x2 |
(
| ||
1+(
|
| x2 |
| 1+x2 |
| 1 |
| x2+1 |
∴f(1)+f(2)+f(3)+…+f(2009)+f(
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 2009 |
=f(1)+[f(2)+f(
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 2009 |
=
| 1 |
| 2 |
=2008
| 1 |
| 2 |
故选:D.
点评:本题考查函数值求解,函数性质.意识到先考虑f(x)+f(
)的结果的特殊性,是本题的关键,精彩之处.也是良好数学素养的体现.
| 1 |
| x |

练习册系列答案
 星级口算天天练系列答案
星级口算天天练系列答案 芒果教辅达标测试卷系列答案
芒果教辅达标测试卷系列答案
相关题目
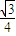 sin x-
sin x- cos x.
cos x.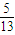 ,x∈[
,x∈[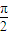 ,π],求函数f (x)的值;
,π],求函数f (x)的值;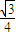 sin x-
sin x- cos x.
cos x.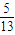 ,x∈[
,x∈[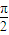 ,π],求函数f (x)的值;
,π],求函数f (x)的值;