题目内容
(09年崇文区期末理)(13分)
射击运动员在双项飞碟比赛中,每轮比赛连续发射两枪,击中两个飞靶得2分,击中一个飞靶得1分,不击中飞靶得0分,某射击运动员在每轮比赛连续发射两枪时,第一枪命中率为 ,第二枪命中率为
,第二枪命中率为 ,
该运动员如进行2轮比赛.
,
该运动员如进行2轮比赛.
(Ⅰ)求该运动员得4分的概率为多少?
(Ⅱ)若该运动员所得分数为 ,求
,求 的分布列及数学期望.
的分布列及数学期望.
【答案】
解析:(I)设运动员得4分的事件为A,
则P(A)=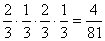 .
----------------5分
.
----------------5分
(Ⅱ)设运动员得i分的事件为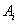 ,
,
ξ的可能取值为0, 1, 2, 3,4 .--------------------------------------------------------6分
P(ξ=0)= P(ξ=4)=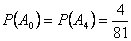 ,
-----------------------------------------8分
,
-----------------------------------------8分
P(ξ= 1) = P(ξ=3) =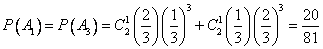 ,--10分
,--10分
P(ξ= 2) =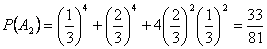 , --
-------------11分
, --
-------------11分
|
ξ |
0 |
1 |
2 |
3 |
4 |
|
P |
|
|
|
|
|
ξ的分布列为:
--------------12分
数学期望 Eξ=0×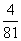 + 1×
+ 1×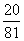 + 2×
+ 2×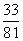 + 3×
+ 3×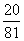 + 4×
+ 4×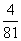 =2.
------13分
=2.
------13分

练习册系列答案
相关题目
