题目内容
(本小题满分10分)
在△ABC中,A、B为锐角,角A、B、C所对的边分别为 、
、 、
、 ,且
,且
 .
.
(1)求角C的值;
(2)若a-b= -1,求
-1,求 、
、 、
、 的值.
的值.
在△ABC中,A、B为锐角,角A、B、C所对的边分别为
 、
、 、
、 ,且
,且
 .
.(1)求角C的值;
(2)若a-b=
 -1,求
-1,求 、
、 、
、 的值.
的值.(1)

(2)a=
 ,b=1,c=
,b=1,c=
解:(1)∵A、B为锐角,sinA= ,sinB=
,sinB=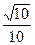 ,
,
∴cosA= =
=
 ,------------1分
,------------1分
cosB= =
= ,--------------2分
,--------------2分
∴cosC=-cos(A+B)=-(cosAcosB-sinAsinB)
=-( ×
× -
- ×
×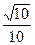 )=
)= .---------------4分
.---------------4分
∵0 <C<π,∴C=
<C<π,∴C= --------------5分
--------------5分
(2)由(1)知C=,∴sinC= . --------6分
. --------6分
由正弦定理==得 a=
a= b=
b= c,即a=
c,即a= b,c=
b,c= b,
b,
∵a-b =
= -1,∴
-1,∴ b-b=
b-b= -1,∴b=1,
-1,∴b=1,
∴a= ,c=
,c= . --------------10分
. --------------10分
 ,sinB=
,sinB=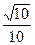 ,
,∴cosA=
 =
=
 ,------------1分
,------------1分cosB=
 =
= ,--------------2分
,--------------2分∴cosC=-cos(A+B)=-(cosAcosB-sinAsinB)
=-(
 ×
× -
- ×
×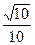 )=
)= .---------------4分
.---------------4分∵0
 <C<π,∴C=
<C<π,∴C= --------------5分
--------------5分(2)由(1)知C=,∴sinC=
 . --------6分
. --------6分由正弦定理==得
 a=
a= b=
b= c,即a=
c,即a= b,c=
b,c= b,
b,∵a-b
 =
= -1,∴
-1,∴ b-b=
b-b= -1,∴b=1,
-1,∴b=1,∴a=
 ,c=
,c= . --------------10分
. --------------10分
练习册系列答案
相关题目
 中,
中,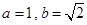 ,
,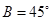 ,则角
,则角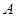 等于
等于
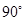

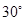
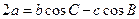
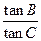 的值;
的值;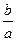 的取值范围是( )
的取值范围是( )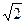 ,
, )
) ,其中
,其中
 ,若
,若 图象中相邻的对称轴间的距离不小于
图象中相邻的对称轴间的距离不小于 ..
.. 的取值范围;
的取值范围; 中,
中, 分别为角
分别为角 的对边.且
的对边.且 ,当
,当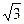 ac,则角B的值为
ac,则角B的值为 B、
B、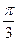 C、
C、 D、
D、
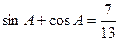 ,则ΔABC的形状是___________.
,则ΔABC的形状是___________.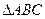 中,
中,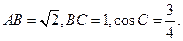
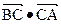 =
= 


 ∶2
∶2