题目内容
【题目】将边长为2正方形ABCD沿对角线BD折成直二面角A﹣BD﹣C,有如下四个判断:
①AC⊥BD
②AB与平面BCD所成60°角
③△ABC是等边三角形
④若A、B、C、D四点在同一个球面上,则该球的表面积为8π
其中正确判断的序号是 .
【答案】①③④
【解析】解:①取BD中点E,连结AE,CE,则AE⊥BD,CE⊥BD,∴BD⊥平面ACE,∴AC⊥BD.故①正确.
②∠ABD为AB与面BCD所成的角为45°,故②错误.
③∵折叠前正方形的边长为2,∴BD=2![]() , ∴AE=CE=
, ∴AE=CE=![]() .
.
∵平面ABD⊥平面BCD,∴AE⊥平面BCD,∴AE⊥CE,∴AC=![]() =2.
=2.
∴△ABC是等边三角形,故③正确.
④∵折叠前正方形的边长为2,则BD=2![]() ,
,
∴EA=EB=EC=ED=![]() .
.
若A、B、C、D四点在同一个球面上,
则球的半径r=![]() ,
,
则该球的表面积S=4π(![]() )2=8π,故④正确,
)2=8π,故④正确,
所以答案是:①③④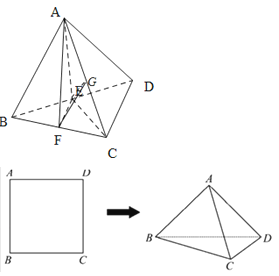
【考点精析】解答此题的关键在于理解命题的真假判断与应用的相关知识,掌握两个命题互为逆否命题,它们有相同的真假性;两个命题为互逆命题或互否命题,它们的真假性没有关系.

练习册系列答案
 A加金题 系列答案
A加金题 系列答案 全优测试卷系列答案
全优测试卷系列答案
相关题目