题目内容
已知f (x)=2x-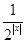
(1)若f (x)=2,求x的值.
(2)若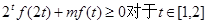 恒成立,求实数m的取值范围.
恒成立,求实数m的取值范围.
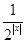
(1)若f (x)=2,求x的值.
(2)若
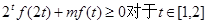 恒成立,求实数m的取值范围.
恒成立,求实数m的取值范围.(1) ;(2)[-5,+∞)
;(2)[-5,+∞)
 ;(2)[-5,+∞)
;(2)[-5,+∞)(1)解方程即可.注意对x讨论去绝对值.
(2)由于 ,所以
,所以 ,然后参数m与变量t分离,转化成函数最值解决.
,然后参数m与变量t分离,转化成函数最值解决.
解:(1)当x<0时f (x)= 0,与x≥0时,f(x)=2x-
由
∴
(2)当t∈[1,2]时,2t(22t-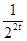 )+m(2t-
)+m(2t- )≥0
)≥0
即m(22t-1)≥-(24t-1) ∵22t-1>0
∴m≥-(22t+1) ∵t∈[1,2]
∴-(1+22t) ∈[-17,-5]
故m的取值范围是[-5,+∞)
(2)由于
 ,所以
,所以 ,然后参数m与变量t分离,转化成函数最值解决.
,然后参数m与变量t分离,转化成函数最值解决.解:(1)当x<0时f (x)= 0,与x≥0时,f(x)=2x-

由

∴

(2)当t∈[1,2]时,2t(22t-
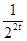 )+m(2t-
)+m(2t- )≥0
)≥0即m(22t-1)≥-(24t-1) ∵22t-1>0
∴m≥-(22t+1) ∵t∈[1,2]
∴-(1+22t) ∈[-17,-5]
故m的取值范围是[-5,+∞)

练习册系列答案
 新课标快乐提优暑假作业陕西旅游出版社系列答案
新课标快乐提优暑假作业陕西旅游出版社系列答案 暑假衔接培优教材浙江工商大学出版社系列答案
暑假衔接培优教材浙江工商大学出版社系列答案
相关题目
 ,且
,且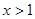 ,则
,则

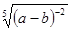 改写成分数指数幂的形式 ( )
改写成分数指数幂的形式 ( )
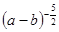
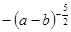
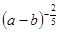
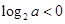 ,
, ,则( ).
,则( ).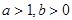

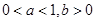

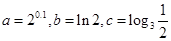 ,则 ( )
,则 ( ) 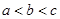
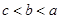
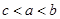
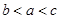
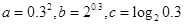 ,则
,则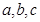 的大小关系为( )
的大小关系为( )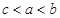

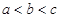
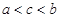
 -
- ·
·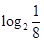 +lg4+2lg5=
+lg4+2lg5=