题目内容
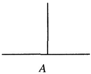
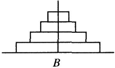
如下图,汉诺塔问题是指有3根杆子A,B,C.B杆上有若干碟子,把所有碟子从B杆移到A杆上,每次只能移动一个碟子,大的碟子不能叠在小的碟子上面.把B杆上的4个碟子全部移到A杆上,最少需要移动( )次. ( )

A.12 B.15 C.17 D.19



A.12 B.15 C.17 D.19
B
把上面三个碟子作为一个整体,移动的顺序是:(1)把上面三个碟子从B杆移到C杆子;(2)把第四个碟子从B移到A;(3)把上面3个碟子从C杆子移到A杆子。
用符号表示为:(B,C) (B,A) (A,C) (B,C) (A,B) (A,C) (B,C) (B,A) (C,A)
(C,B) (A,B) (C,A) (B,C) (BA,) (C,A)共移动15次。故选B
用符号表示为:(B,C) (B,A) (A,C) (B,C) (A,B) (A,C) (B,C) (B,A) (C,A)
(C,B) (A,B) (C,A) (B,C) (BA,) (C,A)共移动15次。故选B

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目

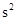 ,将这组数据中的每一个数都乘以2,所得到的一组新数据的方差为( )
,将这组数据中的每一个数都乘以2,所得到的一组新数据的方差为( )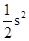
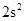
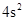
 、第二组
、第二组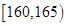 ;…第八组
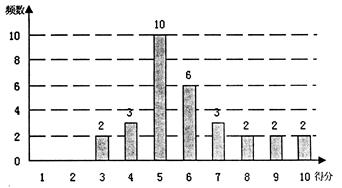
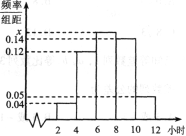
;…第八组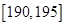 ,右图是按上述分组方法得到的频率分布直方图的一部分,已知第一组与第八组人数相同,第六组、第七组、第八组人数依次构成等差数列.
,右图是按上述分组方法得到的频率分布直方图的一部分,已知第一组与第八组人数相同,第六组、第七组、第八组人数依次构成等差数列.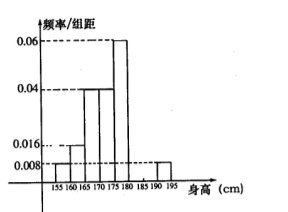
 ,求满足
,求满足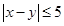 的事件概率.
的事件概率.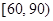 内的学生人数为 .
内的学生人数为 .
 )进行统计,得到如图所示的频率分布直方图,
)进行统计,得到如图所示的频率分布直方图,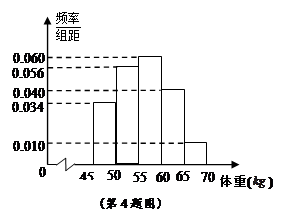
 ,众数为mo,则
,众数为mo,则