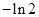题目内容
设 ,函数
,函数 的导函数
的导函数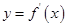 是奇函数,若曲线
是奇函数,若曲线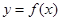 的一条切线的斜率为
的一条切线的斜率为 ,则切点的横坐标是( )
,则切点的横坐标是( )
A. B.
B.
C.  D.
D.
【答案】
C
【解析】解:由题意可得,f′(x)=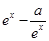 是奇函数,
是奇函数,
∴f′(0)=1-a=0
∴a=1,f(x)=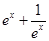 ,f′(x)=
,f′(x)=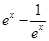 ,
,
∵曲线y=f(x)在(x,y)的一条切线的斜率是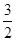 ,
,
∴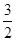 =
=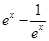 ,
,
解方程可得ex=2,
∴x=ln2.
故答案为C

练习册系列答案
相关题目
 函数
函数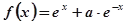 的导函数是
的导函数是 且
且 是奇函数,若曲线
是奇函数,若曲线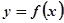 的一条切线的斜率是
的一条切线的斜率是 则切点的横坐标为( )
则切点的横坐标为( ) B.
B. C.
C. D.
D.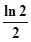
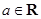 ,函数
,函数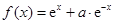 的导函数是
的导函数是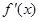 ,且
,且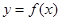 的一条切线的斜率是
的一条切线的斜率是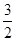 ,则切点的横坐标为( )
,则切点的横坐标为( )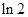 B.
B.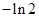 C.
C.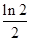 D.
D.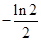
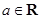 ,函数
,函数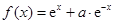 的导函数是
的导函数是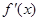 ,且
,且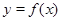 的一条切线的斜率是
的一条切线的斜率是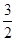 ,则切点的横坐标为
( )
,则切点的横坐标为
( )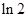 B、
B、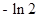 C、
C、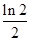 D、
D、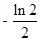
 ,函数
,函数 的导函数
的导函数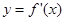 是奇函数,若曲线
是奇函数,若曲线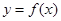 的一条切线斜率为
的一条切线斜率为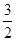 ,则切点的横坐标为 ( )
,则切点的横坐标为 ( )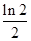 B.
B.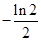 C.
C.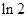 D.
D.