题目内容
若 的取值范围是 .
的取值范围是 .
【答案】分析:通过二倍角公式化简cos2A+cos2B,通过A+B=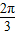 ,进而求出cos2A+cos2B=
,进而求出cos2A+cos2B= cos(2A+
cos(2A+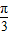 )+1,根据余弦函数的性质得出答案.
)+1,根据余弦函数的性质得出答案.
解答:解:cos2A+cos2B
= (2cos2A-1)+
(2cos2A-1)+ +
+ (2cos2B-1)+
(2cos2B-1)+
= cos2A+
cos2A+ cos2B+1
cos2B+1
∵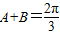
∴B=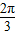 -A
-A
∴ cos2A+
cos2A+ cos2B+1
cos2B+1
= cos2A+
cos2A+ cos(
cos(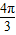 -2A)+1
-2A)+1
= cos2A+
cos2A+ [(-
[(- cos2A)-
cos2A)-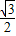 sin2A]+1
sin2A]+1
= (
( cos2A-
cos2A-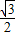 sin2A)+1
sin2A)+1
= cos(2A+
cos(2A+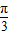 )+1
)+1
即cos2A+cos2B= cos(2A+
cos(2A+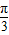 )+1
)+1
∵-1≤cos(2A+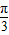 )≤1
)≤1
∴ ≤
≤ cos(2A+
cos(2A+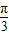 )+1≤
)+1≤
即cos2A+cos2B的取值范围为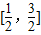
故答案为: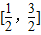
点评:本题主要考查了三角函数中的二倍角和两角和公式的应用.要求应熟练掌握并灵活运用这些公式.
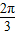 ,进而求出cos2A+cos2B=
,进而求出cos2A+cos2B= cos(2A+
cos(2A+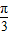 )+1,根据余弦函数的性质得出答案.
)+1,根据余弦函数的性质得出答案.解答:解:cos2A+cos2B
=
 (2cos2A-1)+
(2cos2A-1)+ +
+ (2cos2B-1)+
(2cos2B-1)+
=
 cos2A+
cos2A+ cos2B+1
cos2B+1∵
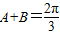
∴B=
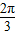 -A
-A∴
 cos2A+
cos2A+ cos2B+1
cos2B+1=
 cos2A+
cos2A+ cos(
cos(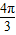 -2A)+1
-2A)+1=
 cos2A+
cos2A+ [(-
[(- cos2A)-
cos2A)-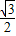 sin2A]+1
sin2A]+1=
 (
( cos2A-
cos2A-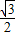 sin2A)+1
sin2A)+1=
 cos(2A+
cos(2A+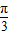 )+1
)+1即cos2A+cos2B=
 cos(2A+
cos(2A+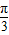 )+1
)+1∵-1≤cos(2A+
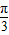 )≤1
)≤1∴
 ≤
≤ cos(2A+
cos(2A+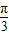 )+1≤
)+1≤
即cos2A+cos2B的取值范围为
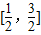
故答案为:
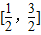
点评:本题主要考查了三角函数中的二倍角和两角和公式的应用.要求应熟练掌握并灵活运用这些公式.

练习册系列答案
 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案
相关题目
 的取值范围是( )
的取值范围是( ) 的取值范围是(
)
的取值范围是(
)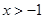 B.
B.
 C.
C.
 D.
D.

 中,点D在线段BC的延长线上,且
中,点D在线段BC的延长线上,且 ,点O在线段CD上(与点C、D不重合),若
,点O在线段CD上(与点C、D不重合),若 的取值范围是 (
)
的取值范围是 (
) B.
B. C.
C. D.
D.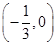
 若
若 的取值范围是 ( )
的取值范围是 ( ) B.
B. C.
C. D.
D.