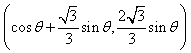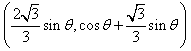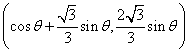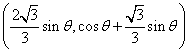题目内容
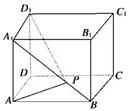如图所示，在单位正方体ABCD-A1B1C1D1的面对角线A1B上存在一点P使得AP+D1P取得最小值，则此最小值为（ ）| A、2 | ||||||
B、
| ||||||
C、2+
| ||||||
D、
|
分析：把对角面A1C绕A1B旋转至A1BC′D1′，使其与△AA1B在同一平面上，连接AD1′并求出，就是最小值．
解答：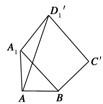
解：如图所示，把对角面A1C绕A1B旋转至A1BC′D1′，
使其与△AA1B在同一平面上，连接AD1′，
则AD1′=
=
为所求的最小值．
故选D．
解：如图所示，把对角面A1C绕A1B旋转至A1BC′D1′，使其与△AA1B在同一平面上，连接AD1′，
则AD1′=
| 1+1-2×1×1×cos135° |
2+
|
故选D．
点评：本题考查棱柱的结构特征，考查计算能力，空间想象能力，是基础题．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
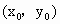为极点，以x轴的正方向为极轴方向建立极坐标系如图所示，写出平面上点的直角坐标和极坐标的变换公式(假设极坐标系和直角坐标系中的长度单位相同)．
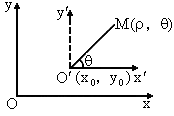
(其中
分别是斜坐标系x轴、y轴正方向上的单位向量，x、y∈R，O为坐标原点)，则有序实数对(x，y)称为点P的斜坐标．如图所示，在平面斜坐标系xOy中，若∠xOy＝120°，点A(1，0)，P为单位圆上一点，且∠AOP＝
，点P在平面斜坐标系中的坐标是
中，若
（其中
、
分别是斜坐标系
轴、
轴正方向上的单位向量，
，
为坐标原点），则有序实数对
称为点
的斜坐标. 如图所示,在平面斜坐标系
，点
，
，点
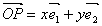（其中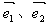
分别是斜坐标系x轴、y轴正方向上的单位向量，x、y∈R，O为坐标原点），则有序实数对（x，y）称为点P的斜坐标。如图所示，在平面斜坐标系xOy中，若∠xOy=120°，点A（1，0），P为单位圆上一点，且∠AOP=θ，点P在平面斜坐标系中的坐标是
中，若
（其中
、
分别是斜坐标系
轴、
轴正方向上的单位向量，
，
为坐标原点），则有序实数对
称为点
的斜坐标. 如图所示,在平面斜坐标系
，点
，
，点
