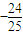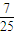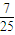题目内容
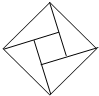 在北京召开的第24届国际数学家大会会标如图所示,它是由四个相同的直角三角形与中间的小正方形拼成的一个大正方形.若直角三角形中较小的锐角记作θ,大正方形的面积是1,小正方形的面积是
在北京召开的第24届国际数学家大会会标如图所示,它是由四个相同的直角三角形与中间的小正方形拼成的一个大正方形.若直角三角形中较小的锐角记作θ,大正方形的面积是1,小正方形的面积是| 1 |
| 25 |
| A、1 | ||
B、-
| ||
C、
| ||
D、-
|
分析:由已知大会会标由4个相同的直角三角形与中间的面积是
小正方形拼成的一个面积是1大正方形,我们可以设角形短直角边为x,然后根据余弦定理(在直角三角形中也可称为勾股定理),我们构造出关于x的方程,解方程求出三角形各边长,即可得到θ的各三角函数值,进而得到sin2θ-cos2θ的值
| 1 |
| 25 |
解答:解:设三角形短直角边为x
∵S小正方形=
∴小正方形边长=
∴直角三角形另一条直角边为x+
∵S大正方形=1
∴大正方形边长=1
根据勾股定理,x2+(x+
)2=12
解得x=
∴sinθ=
,cosθ=
∴sin2θ-cos2θ=-
故选D
∵S小正方形=
| 1 |
| 25 |
∴小正方形边长=
| 1 |
| 5 |
∴直角三角形另一条直角边为x+
| 1 |
| 5 |
∵S大正方形=1
∴大正方形边长=1
根据勾股定理,x2+(x+
| 1 |
| 5 |
解得x=
| 3 |
| 5 |
∴sinθ=
| 3 |
| 5 |
| 4 |
| 5 |
∴sin2θ-cos2θ=-
| 7 |
| 25 |
故选D
点评:本题考查的知识点是余弦定理,方程思想,根据已知,设出求知的边长,根据余弦定理(在直角三角形中也可称为勾股定理),我们构造出关于x的方程,是解答本题的关键.

练习册系列答案
 一线名师提优试卷系列答案
一线名师提优试卷系列答案
相关题目
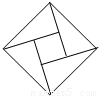 在北京召开的第24届国际数学家大会会标如图所示,它是由四个相同的直角三角形与中间的小正方形拼成的一个大正方形.若直角三角形中较小的锐角记作θ,大正方形的面积是1,小正方形的面积是
在北京召开的第24届国际数学家大会会标如图所示,它是由四个相同的直角三角形与中间的小正方形拼成的一个大正方形.若直角三角形中较小的锐角记作θ,大正方形的面积是1,小正方形的面积是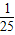 ,则sin2θ-cos2θ的值等于( )
,则sin2θ-cos2θ的值等于( )
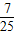
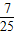
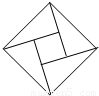 在北京召开的第24届国际数学家大会会标如图所示,它是由四个相同的直角三角形与中间的小正方形拼成的一个大正方形.若直角三角形中较小的锐角记作θ,大正方形的面积是1,小正方形的面积是
在北京召开的第24届国际数学家大会会标如图所示,它是由四个相同的直角三角形与中间的小正方形拼成的一个大正方形.若直角三角形中较小的锐角记作θ,大正方形的面积是1,小正方形的面积是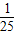 ,则sin2θ-cos2θ的值等于( )
,则sin2θ-cos2θ的值等于( )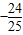
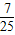

 在北京召开的第24届国际数学家大会会标如图所示,它是由四个相同的直角三角形与中间的小正方形拼成的一个大正方形.若直角三角形中较小的锐角记作θ,大正方形的面积是1,小正方形的面积是
在北京召开的第24届国际数学家大会会标如图所示,它是由四个相同的直角三角形与中间的小正方形拼成的一个大正方形.若直角三角形中较小的锐角记作θ,大正方形的面积是1,小正方形的面积是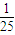 ,则sin2θ-cos2θ的值等于( )
,则sin2θ-cos2θ的值等于( )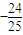
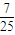
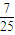
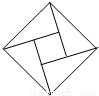 在北京召开的第24届国际数学家大会会标如图所示,它是由四个相同的直角三角形与中间的小正方形拼成的一个大正方形.若直角三角形中较小的锐角记作θ,大正方形的面积是1,小正方形的面积是
在北京召开的第24届国际数学家大会会标如图所示,它是由四个相同的直角三角形与中间的小正方形拼成的一个大正方形.若直角三角形中较小的锐角记作θ,大正方形的面积是1,小正方形的面积是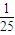 ,则sin2θ-cos2θ的值等于( )
,则sin2θ-cos2θ的值等于( )