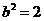题目内容
已知椭圆与双曲线![]() 有公共的焦点,且椭圆过点P(0,2)。
有公共的焦点,且椭圆过点P(0,2)。
(1)求椭圆方程的标准方程;
(2)若直线![]() 与双曲线的渐近线平行,且与椭圆相切,求直线
与双曲线的渐近线平行,且与椭圆相切,求直线![]() 的方程。
的方程。
解:(1)设椭圆方程为![]() (
(![]() >b>0).
>b>0).
![]() 双曲线
双曲线![]() 的焦点坐标分别为(– 2 ,0)(2,0), ……2分
的焦点坐标分别为(– 2 ,0)(2,0), ……2分
![]() 椭圆焦点坐标分别为(– 2 ,0)(2,0),∴c=2,即a2 = b2 + 4,……4分
椭圆焦点坐标分别为(– 2 ,0)(2,0),∴c=2,即a2 = b2 + 4,……4分
又椭圆过点P(0,2),∴b2 = 4,得a2 = 8
∴所求椭圆方程的标准方程为 ![]() . …… 6分
. …… 6分
(2)双曲线渐近线方程:y = ![]() x ,
x ,
故设直线![]() :y =
:y = ![]() x + m, …… 8分
x + m, …… 8分
代入椭圆方程得:7x2 ±4![]() mx + 2m2 – 8 =0, ……10分
mx + 2m2 – 8 =0, ……10分
由相切得:△=48m2 – 28(2m2 – 8 )= 0, 解得m = ![]() ……12分
……12分
∴直线![]() 的方程是:y =
的方程是:y = ![]() x
x![]() …… 13分
…… 13分

练习册系列答案
相关题目
 与双曲线
与双曲线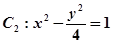 有公共的焦点,
有公共的焦点, 的一条渐近线与以
的一条渐近线与以 的长轴为直径的圆相交于A,B两点,若
的长轴为直径的圆相交于A,B两点,若 =
=
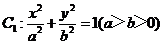 与双曲线
与双曲线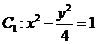 有公共的焦点,
有公共的焦点,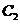 的一条渐近线与以
的一条渐近线与以 的长轴为直径的圆相交于
的长轴为直径的圆相交于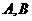 两点,若
两点,若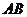 三等分,则
三等分,则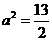 (B)
(B)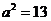 (C)
(C)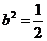 (D)
(D)