题目内容
(1)点A(2,-4)在以原点为顶点,坐标轴为对称轴的抛物线上,求抛物线方程;(2)已知双曲线C经过点(1,1),它渐近线方程为y=±
| 3 |
分析:(1)点A(2,-4)在第四象限,设抛物线方程为 y2=2px ①,或 x2=-2py ②,把点的坐标代入求得p值,即得到抛物线方程.
(2)根据渐近线方程,设双曲线的方程为 y2-3x2=λ,将点(1,1)代入可得 λ 值,从而得到双曲线方程.
(2)根据渐近线方程,设双曲线的方程为 y2-3x2=λ,将点(1,1)代入可得 λ 值,从而得到双曲线方程.
解答:解:(1)点A(2,-4)在第四象限,设抛物线方程为 y2=2px ①,或 x2=-2py ②,
将点A(2,-4)代入①解得 p=4,将点A(2,-4)代入②解得 p=
,
故抛物线的方程为:y2=8x,或 x2=-y.
(2)解:设双曲线的方程为 y2-3x2=λ,将点(1,1)代入可得 λ=-2,
故答案为
-
=1.
将点A(2,-4)代入①解得 p=4,将点A(2,-4)代入②解得 p=
| 1 |
| 2 |
故抛物线的方程为:y2=8x,或 x2=-y.
(2)解:设双曲线的方程为 y2-3x2=λ,将点(1,1)代入可得 λ=-2,
故答案为
| 3x2 |
| 2 |
| y2 |
| 2 |
点评:本题考查抛物线、双曲线的标准方程,以及双曲线、抛物线的简单性质的应用,体现了分类讨论的数学思想,设出抛物线的标准方程是解题的易错点,容易漏掉另一种情况.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 x,求双曲线C的标准方程.
x,求双曲线C的标准方程.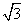 x,求双曲线C的标准方程。
x,求双曲线C的标准方程。 x,求双曲线C的标准方程.
x,求双曲线C的标准方程.