Question

 已知函数f (x)＝x³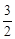＋(1－a)x²－3ax＋1，a＞0．

(Ⅰ) 证明：对于正数a，存在正数p，使得当x∈[0，p]时，有－1≤f (x)≤1；

(Ⅱ) 设(Ⅰ)中的p的最大值为g(a)，求g(a)的最大值．

 

Answer 1

【答案】

(Ⅰ)见解析  (Ⅱ)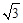

【解析】

试题分析：(Ⅰ) 由于 f ′(x)＝3x²＋3(1－a)x－3a＝3(x＋1)(x－a)，且a＞0，

故f (x)在[0，a]上单调递减，在[a，＋∞)上单调递增．又

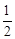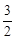f (0)＝1，  f (a)＝－a³－a²＋1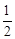＝(1－a)(a＋2) ²－1．

当f (a)≥－1时，取p＝a．

此时，当x∈[0，p]时有－1≤f (x)≤1成立．

当f (a)＜－1时，由于f (0)＋1＝2＞0，f (a)＋1＜0，

故存在p∈(0，a)使得f (p)＋1＝0．

此时，当x∈[0，p]时有－1≤f (x)≤1成立．

综上，对于正数a，存在正数p，使得当x∈[0，p]时，有－1≤f (x)≤1．

(Ⅱ) 由(Ⅰ)知f (x)在[0，＋∞)上的最小值为f (a)．

当0＜a≤1时，f (a)≥－1，则g(a)是方程f (p)＝1满足p＞a的实根，

即2p²+3(1－a)p－6a＝0满足p＞a的实根，所以

g(a)＝．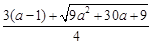

又g(a)在(0，1]上单调递增，故

g(a)_max＝g(1)＝．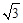

当a＞1时，f (a)＜－1．

由于f (0)＝1，f (1)＝(1－a)－1＜－1，故

[0，p]Ì [0，1]．

此时，g(a)≤1．

综上所述，g(a)的最大值为．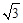

考点：导数的性质和应用

点评：本题主要考查利用导数研究函数的性质等基础知识，同时考查推理论证能力，分类讨论等综合解题能力和创新意识。