题目内容

4．用min{a，b}表示a，b两个数中的最小值，设f（x）=min{x+2，10-x}，则当x=4时，f（x）的最大值为6．

分析 在坐标系内画出函数y=x+2，y=10-x的图象，根据图象求出f（x）的最大值．

解答 解：在坐标系内画出函数y=x+2，y=10-x的图象，如图；
由图象知，f（x）=min{x+2，10-x}=$\left\{\begin{array}{l}{x+2，x≤4}\\{10-x，x＞4}\end{array}\right.$，
∴f（x）的最大值为f（x）max=f（4）=6，
故答案为：4，6．

点评 本题考查了新定义的函数的最值问题，结合图象，容易得出结论．

练习册系列答案
相关题目
14．设f（x）=$\left\{{\begin{array}{l}{{{log}_2}x，}&{x＞0}\\{{2^x}，}&{x≤0}\end{array}}$，则$f（f（\frac{1}{2}））$的值为$\frac{1}{2}$，不等式f（x）＞$\frac{1}{2}$的解集为$（-1，0]∪（\sqrt{2}，+∞）$．
15．函数y=lg（4-2x）的定义域是（　　）
A．（2，4）B．（2，+∞）C．（0，2）D．（-∞，2）
12．设命题p：?x＞1，x2-x+1＞0，则?p为（　　）
A．?x≤1，x2-x+1≤0B．?x＞1，x2-x+1≤0C．?x＞1，x2-x+1≤0D．?x≤1，x2-x+1＞0
19．已知函数y=f（x+1）的图象过点（3，2），则函数y=-f（x）的图象一定过点（　　）
A．（2，-2）B．（2，2）C．（-4，2）D．（4，-2）
9．函数y=lg（-x2-2x+8）的单调递减区间是（　　）
A．（-∞，-1）B．（-1，2）C．（-4，-1）D．（-1，+∞）
16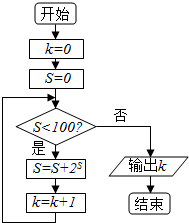．如果执行如图所示的程序，那么输出的值k=（　　）
A．3B．4C．5D．6
13．已知命题p：（x+1）（2-x）≥0，命题q：x2-2x-（a2-1）≤0（a＞0），若￢p是￢q的必要不充分条件，则a的取值范围为[2，+∞）．
14．已知数列{an}满足：a1=$\frac{1}{2}$，an+1=$\frac{1}{2}$an+2-n（n∈N*）．
（1）证明：数列{2n•an}是等差数列；
（2）求数列{an}的前n项和Sn．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网