题目内容
下列结论中正确结论的序号是
(1)函数y=sinx在第一象限单调递增;
(2)函数f(x)=sin(
+
)是偶函数;
(3)已知f(x)=3sin(ωx+φ)+1(ω>0,|φ|<π),且对任意实数t都有f(t+
)=f(
-t),设g(x)=3cos(ωx+φ)-1,则g(
)=-1
(4)设α,β是锐角三角形两个内角,则sinα<cosβ.
(2)(3)
(2)(3)
.(1)函数y=sinx在第一象限单调递增;
(2)函数f(x)=sin(
| 2x |
| 3 |
| 7π |
| 2 |
(3)已知f(x)=3sin(ωx+φ)+1(ω>0,|φ|<π),且对任意实数t都有f(t+
| π |
| 3 |
| π |
| 3 |
| π |
| 3 |
(4)设α,β是锐角三角形两个内角,则sinα<cosβ.
分析:(1)利用正弦函数的单调性可判断y=sinx在第一象限单调递增的正误;
(2)利用诱导公式可知f(x)=sin(
+
)=sin(
x-
)=-cos
x,从而可判断(2)的正误;
(3)由已知得,y=f(x)关于x=
对称,于是可由g(x)=3cos(ωx+φ)-1,求得g(
),从而可判断其正误;
(4)利用诱导公式与正弦函数的单调性即可判断(4).
(2)利用诱导公式可知f(x)=sin(
| 2x |
| 3 |
| 7π |
| 2 |
| 2 |
| 3 |
| π |
| 2 |
| 2 |
| 3 |
(3)由已知得,y=f(x)关于x=
| π |
| 3 |
| π |
| 3 |
(4)利用诱导公式与正弦函数的单调性即可判断(4).
解答:解:(1)函数y=sinx在(0,
)上单调递增,但并不是在第一象限单调递增,故(1)错误;
(2)∵f(x)=sin(
+
)=sin(
x-
)=-cos
x,
∴f(-x)=-cos(-
x)=-cos
x=-f(x),
∴函数f(x)=sin(
+
)是偶函数,正确;
(3)∵f(t+
)=f(
-t),
∴y=f(x)关于x=
对称,
∴sin(ωx+φ)=±1,
∴cos(ωx+φ)=0,
∴g(
)=-1,故(3)正确;
(4)∵α,β是锐角三角形两个内角,
∴
<α+β<π,
∴
>β>
-α>0,
∴cosβ<cos(
-α)=sinα,故(4)错误;
综上所述,(2)(3)正确;
故答案为:(2)(3).
| π |
| 2 |
(2)∵f(x)=sin(
| 2x |
| 3 |
| 7π |
| 2 |
| 2 |
| 3 |
| π |
| 2 |
| 2 |
| 3 |
∴f(-x)=-cos(-
| 2 |
| 3 |
| 2 |
| 3 |
∴函数f(x)=sin(
| 2x |
| 3 |
| 7π |
| 2 |
(3)∵f(t+
| π |
| 3 |
| π |
| 3 |
∴y=f(x)关于x=
| π |
| 3 |
∴sin(ωx+φ)=±1,
∴cos(ωx+φ)=0,
∴g(
| π |
| 3 |
(4)∵α,β是锐角三角形两个内角,
∴
| π |
| 2 |
∴
| π |
| 2 |
| π |
| 2 |
∴cosβ<cos(
| π |
| 2 |
综上所述,(2)(3)正确;
故答案为:(2)(3).
点评:本题考查正弦函数的奇偶性,对称性与单调性,考查转化思想与综合运算能力,属于中档题.

练习册系列答案
 小学教材全测系列答案
小学教材全测系列答案 小学数学口算题卡脱口而出系列答案
小学数学口算题卡脱口而出系列答案
相关题目
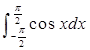 的值为2;
的值为2; ,则
,则 与
与 的夹角为钝角;
的夹角为钝角; ,则不等式
,则不等式 成立的概率是
成立的概率是 ;
; 的最小值为2.
的最小值为2. ”的充分不必要条件( )
”的充分不必要条件( ) ”的充分不必要条件( )
”的充分不必要条件( ) ”的充分不必要条件( )
”的充分不必要条件( )