题目内容
已知f(x)=2asin(2x+ )-a+b,a,b∈Q.当x
)-a+b,a,b∈Q.当x 时,f(x)∈[-3,
时,f(x)∈[-3, ].
].(1)求f(x)的解析式;
(2)用列表描点法作出f(x)在[0,π]上的图象;
(3)简述由函数y=sin(2x)的图象经过怎样的变换可得到函数f(x)的图象.
【答案】分析:(1)由三角函数的性质求出用参数表示的函数的最值,由于函数的值域已知,故此两区间相等,故左端点与左端点相等,右端点与右端点相等,由此得到参数的方程,解出参数值即可.
(2)通过列表,描点连线,画出函数在[0,π]上的图象.
(3)函数y=sin(2x)经过左右平移,伸长到原来的2倍,通过上下平移即可得到函数的解析式.
解答:解:(1)∵ ,
,
∴2x+ ∈[
∈[ ,
, ],
],
∴sin(2x+ )∈[-1,
)∈[-1, ],
],
∴2asin(2x+ )∈[-2a,
)∈[-2a, a],
a],
∴f(x)∈[-3a+b, a-a+b],又f(x)∈[-3,
a-a+b],又f(x)∈[-3, ].
].
∴ ,解得
,解得  .
.
f(x)的解析式:f(x)=2sin(2x+ )-1.
)-1.
(2)函数f(x)=2sin(2x+ )-1在[0,π]列表,画出图象,如图.
)-1在[0,π]列表,画出图象,如图.


(3)函数y=sin(2x)经过向左平移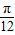 ,伸长到原来的2倍,纵坐标不变,向下平移1单位,即可得到函数的解析式2sin(2x+
,伸长到原来的2倍,纵坐标不变,向下平移1单位,即可得到函数的解析式2sin(2x+ )-1.
)-1.
点评:本题考点是三角函数的最值,考查利用三角函数的最值建立方程求参数,求三角函数的最值一般需要先研究三角函数的单调性,由单调性求最值,本题求最值采用了求复合函数最值常用的方法;注意函数图象的平移,五点法作图的基本方法.
(2)通过列表,描点连线,画出函数在[0,π]上的图象.
(3)函数y=sin(2x)经过左右平移,伸长到原来的2倍,通过上下平移即可得到函数的解析式.
解答:解:(1)∵
 ,
,∴2x+
 ∈[
∈[ ,
, ],
],∴sin(2x+
 )∈[-1,
)∈[-1, ],
],∴2asin(2x+
 )∈[-2a,
)∈[-2a, a],
a],∴f(x)∈[-3a+b,
 a-a+b],又f(x)∈[-3,
a-a+b],又f(x)∈[-3, ].
].∴
 ,解得
,解得  .
.f(x)的解析式:f(x)=2sin(2x+
 )-1.
)-1.(2)函数f(x)=2sin(2x+
 )-1在[0,π]列表,画出图象,如图.
)-1在[0,π]列表,画出图象,如图.

(3)函数y=sin(2x)经过向左平移
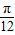 ,伸长到原来的2倍,纵坐标不变,向下平移1单位,即可得到函数的解析式2sin(2x+
,伸长到原来的2倍,纵坐标不变,向下平移1单位,即可得到函数的解析式2sin(2x+ )-1.
)-1.点评:本题考点是三角函数的最值,考查利用三角函数的最值建立方程求参数,求三角函数的最值一般需要先研究三角函数的单调性,由单调性求最值,本题求最值采用了求复合函数最值常用的方法;注意函数图象的平移,五点法作图的基本方法.

练习册系列答案
相关题目
 )-a+b,a,b∈Q.当x
)-a+b,a,b∈Q.当x 时,f(x)∈[-3,
时,f(x)∈[-3, ].
]. )+2a+b,x∈[
)+2a+b,x∈[ ,
, ],是否存在常数a,b∈Q时,使得f(x)的值域为[-3,
],是否存在常数a,b∈Q时,使得f(x)的值域为[-3, -1]?若存在,求出a,b的值,若不存在,说明理由.
-1]?若存在,求出a,b的值,若不存在,说明理由. ,
, ]内有实数根,求实数a的范围.
]内有实数根,求实数a的范围.