题目内容
设数列{an}的各项均为正数,前n项和为Sn,已知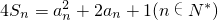 .
.
(1)证明数列{an}是等差数列,并求其通项公式;
(2)证明:对任意m、k、p∈N*,m+p=2k,都有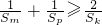 ;
;
(3)对于(2)中的命题,对一般的各项均为正数的等差数列还成立吗?如果成立,请证明你的结论,如果不成立,请说明理由.
解:(1)∵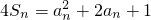 ,∴当n≥2时,
,∴当n≥2时, .
.
两式相减得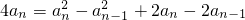 ,
,
∴(an+an-1)(an-an-1-2)=0,
∵an>0,∴an-an-1=2,
又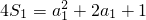 ,∴a1=1,
,∴a1=1,
∴{an}是以a1=1为首项,d=2为公差的等差数列.
∴an=2n-1;
(2)由(1)知 ,
,
∴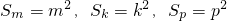 ,
,
于是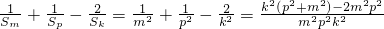
=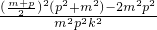
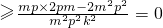 ,
,
∴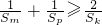 ;
;
(3)结论成立,证明如下:
设等差数列{an}的首项为a1,公差为d,则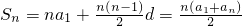 ,
,
于是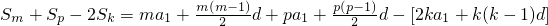
=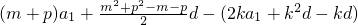 ,
,
将m+p=2k代入得,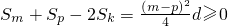 ,
,
∴Sm+Sp≥2Sk,
又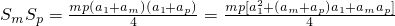
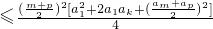
=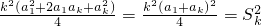 ,
,
∴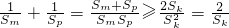 .
.
分析:(1)由所给等式得,当n≥2时, ,然后两式作差得an-an-1=2,由此可判断数列{an}是等差数列,利用通项公式即可求得;
,然后两式作差得an-an-1=2,由此可判断数列{an}是等差数列,利用通项公式即可求得;
(2)利用等差数列求和公式表示出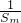 +
+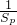 -
-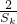 ,再用基本不等式证明该式大于等于0即可;
,再用基本不等式证明该式大于等于0即可;
(3)先用作差法证明Sm+Sp≥2Sk,再用基本不等式证明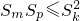 ,由此即可证明结论;
,由此即可证明结论;
点评:本题考查等差数列的求和公式、通项公式,基本不等式的应用,考查学生综合运用所学知识分析解决问题的能力.
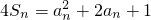 ,∴当n≥2时,
,∴当n≥2时, .
.两式相减得
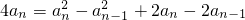 ,
,∴(an+an-1)(an-an-1-2)=0,
∵an>0,∴an-an-1=2,
又
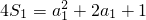 ,∴a1=1,
,∴a1=1,∴{an}是以a1=1为首项,d=2为公差的等差数列.
∴an=2n-1;
(2)由(1)知
 ,
,∴
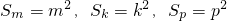 ,
,于是
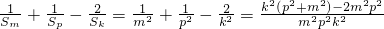
=
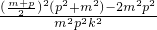
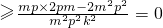 ,
,∴
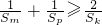 ;
;(3)结论成立,证明如下:
设等差数列{an}的首项为a1,公差为d,则
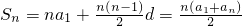 ,
,于是
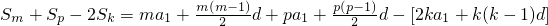
=
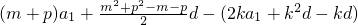 ,
,将m+p=2k代入得,
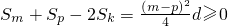 ,
,∴Sm+Sp≥2Sk,
又
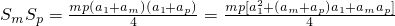
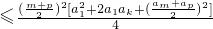
=
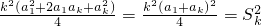 ,
,∴
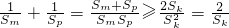 .
.分析:(1)由所给等式得,当n≥2时,
 ,然后两式作差得an-an-1=2,由此可判断数列{an}是等差数列,利用通项公式即可求得;
,然后两式作差得an-an-1=2,由此可判断数列{an}是等差数列,利用通项公式即可求得;(2)利用等差数列求和公式表示出
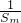 +
+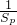 -
-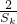 ,再用基本不等式证明该式大于等于0即可;
,再用基本不等式证明该式大于等于0即可;(3)先用作差法证明Sm+Sp≥2Sk,再用基本不等式证明
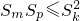 ,由此即可证明结论;
,由此即可证明结论;点评:本题考查等差数列的求和公式、通项公式,基本不等式的应用,考查学生综合运用所学知识分析解决问题的能力.

练习册系列答案
 口算小状元口算速算天天练系列答案
口算小状元口算速算天天练系列答案
相关题目