题目内容
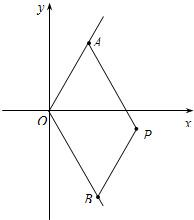 如图,A(m,
如图,A(m,| 3 |
| 3 |
| OA |
| OB |
| 1 |
| 2 |
| OP |
| OA |
| OB |
(Ⅰ)求m•n的值;
(Ⅱ)求P点的轨迹C的方程,并说明它表示怎样的曲线?
(Ⅲ)若直线l过点E(2,0)交(Ⅱ)中曲线C于M、N两点,且
| ME |
| EN |
分析:(I)由向量数量积
•
=-
的坐标运算即可求得m•n的值;
(II)欲求P点的轨迹C的方程,设点P(x,y),只须求出其坐标x,y的关系式即可,由题意向量关系将x,y用m,n表示,最后消去m,n得到一个关系式,即得点P的轨迹方程.
(III)设直线l的方程为x=ty+2,将其代入C的方程得到一个一元二次方程,利用根与系数的关系结合向量运算即可求得t值,从而求得l的方程.
| OA |
| OB |
| 1 |
| 2 |
(II)欲求P点的轨迹C的方程,设点P(x,y),只须求出其坐标x,y的关系式即可,由题意向量关系将x,y用m,n表示,最后消去m,n得到一个关系式,即得点P的轨迹方程.
(III)设直线l的方程为x=ty+2,将其代入C的方程得到一个一元二次方程,利用根与系数的关系结合向量运算即可求得t值,从而求得l的方程.
解答:解:(Ⅰ)由已知得
•
=(m,
m)•(n,-
n)(1分)
=-2mn=-
∴m•n=
(4分)
(Ⅱ)设P点坐标为(x,y)(x>0),由
=
+
得(x,y)=(m,
m)+(n,-
n)=(m+n,
(m-n))(5分)
∴
消去m,n可得x2-
=4mn,又因mn=
(8分)
∴P点的轨迹方程为x2-
=1(x>0)
它表示以坐标原点为中心,焦点在x轴上,且实轴长为2,焦距为4的双曲线x2-
=1的右支(9分)
(Ⅲ)设直线l的方程为x=ty+2,将其代入C的方程得3(ty+2)2-y2=3
即(3t2-1)y2+12ty+9=0
易知(3t2-1)≠0(否则,直线l的斜率为±
,它与渐近线平行,不符合题意)
又△=144t2-36(3t2-1)=36(t2+1)>0
设M(x1,y1),N(x2,y2),则y1+y2=
,y1y2=
∵l与C的两个交点M,N在y轴的右侧
x1x2=(ty1+2)(ty2+2)
=t2y1y2+2t(y1+y2)+4
=t2•
+2t•
+4
=-
>0
∴3t2-1<0,即0<t2<
又由x1+x2>0同理可得0<t2<
(11分)
由
=3
得(2-x1,-y1)=3(2-x2,y2)
∴
由y1+y2=-3y2+y2=-2y2=-
得y2=
由y1y2=(-3y2)y2=-3
=
得
=-
消去y2得
=-
解之得:t2=
,满足0<t2<
(13分)
故所求直线l存在,其方程为:
x-y-2
=0或
x+y-2
=0(14分)
| OA |
| OB |
| 3 |
| 3 |
=-2mn=-
| 1 |
| 2 |
∴m•n=
| 1 |
| 4 |
(Ⅱ)设P点坐标为(x,y)(x>0),由
| OP |
| OA |
| OB |
得(x,y)=(m,
| 3 |
| 3 |
| 3 |
∴
|
| y2 |
| 3 |
| 1 |
| 4 |
∴P点的轨迹方程为x2-
| y2 |
| 3 |
它表示以坐标原点为中心,焦点在x轴上,且实轴长为2,焦距为4的双曲线x2-
| y2 |
| 3 |
(Ⅲ)设直线l的方程为x=ty+2,将其代入C的方程得3(ty+2)2-y2=3
即(3t2-1)y2+12ty+9=0
易知(3t2-1)≠0(否则,直线l的斜率为±
| 3 |
又△=144t2-36(3t2-1)=36(t2+1)>0
设M(x1,y1),N(x2,y2),则y1+y2=
| -12t |
| 3t2-1 |
| 9 |
| 3t2-1 |
∵l与C的两个交点M,N在y轴的右侧
x1x2=(ty1+2)(ty2+2)
=t2y1y2+2t(y1+y2)+4
=t2•
| 9 |
| 3t2-1 |
| -12t |
| 3t2-1 |
=-
| 3t2+4 |
| 3t2-1 |
∴3t2-1<0,即0<t2<
| 1 |
| 3 |
又由x1+x2>0同理可得0<t2<
| 1 |
| 3 |
由
| ME |
| EN |
∴
|
由y1+y2=-3y2+y2=-2y2=-
| 12t |
| 3t2-1 |
| 6t |
| 3t2-1 |
由y1y2=(-3y2)y2=-3
| y | 2 2 |
| 9 |
| 3t2-1 |
| y | 2 2 |
| 3 |
| 3t2-1 |
消去y2得
| 36t2 |
| (3t2-1)2 |
| 3 |
| 3t2-1 |
解之得:t2=
| 1 |
| 15 |
| 1 |
| 3 |
故所求直线l存在,其方程为:
| 15 |
| 5 |
| 15 |
| 5 |
点评:本小题主要考查曲线与方程,直线和圆锥曲线等基础知识,以及求直线方程的基本技能和综合运用数学知识解决问题的能力.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
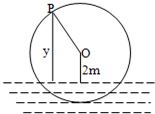 如图为一半径为3m的水轮,水轮中心O距水面2m,已知水轮每分钟旋转4圈,水轮上的点P到水面距离y(m)与时间x(t)满足函数关系y=Asin(ωx+φ)+2则( )
如图为一半径为3m的水轮,水轮中心O距水面2m,已知水轮每分钟旋转4圈,水轮上的点P到水面距离y(m)与时间x(t)满足函数关系y=Asin(ωx+φ)+2则( )A、ω=
| ||
B、ω=
| ||
C、ω=
| ||
D、ω=
|
 为一半径是3m的水轮,水轮圆心O距离水面2m,已知水轮每分钟旋转4圈,水轮上的点P到水面的距离y(m)与时间t(s)满足函数关系y=Asin(ωt+?)+2(ω>0,A>0),则ω=
为一半径是3m的水轮,水轮圆心O距离水面2m,已知水轮每分钟旋转4圈,水轮上的点P到水面的距离y(m)与时间t(s)满足函数关系y=Asin(ωt+?)+2(ω>0,A>0),则ω= 则(
)
则(
)
 B.
B. C.
C.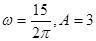 D.
D.

 ,A=5
,A=5 ,A=5
,A=5 ,A=3
,A=3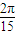 ,A=3
,A=3