题目内容
2.已知$f(x)=(1+\frac{1}{tanx}){sin^2}x-2sin(x+\frac{π}{4})sin(x-\frac{π}{4})$(1)若tanα=2,求f(α)的值;
(2)已知sinθ,cosθ是方程x2-ax+a=0的两根,求f(θ)-$\frac{1}{2}cos2θ-\frac{1}{2}$的值.
分析 (1)利用同角三角函数的基本关系式以及诱导公式两角和与差的三角函数化简函数的表达式,通过tanα=2求出结果即可.
(2)利用已知条件求出a,然后求解f(θ)-$\frac{1}{2}cos2θ-\frac{1}{2}$的值.
解答 解:(1)$f(x)=(1+\frac{1}{tanx}){sin^2}x-2sin(x+\frac{π}{4})sin(x-\frac{π}{4})$
=$(si{n}^{2}x+sinxcosx)+2sin(x+\frac{π}{4})cos(x+\frac{π}{4})$
=$\frac{1-cos2x}{2}+\frac{1}{2}sin2x+sin(2x+\frac{π}{2})$
=$\frac{1}{2}$$(sin2x+cos2x)+\frac{1}{2}$,
∵tanx=2,∴$sin2x=\frac{2sinxcosx}{{sin}^{2}x+{cos}^{2}x}$=$\frac{2tanx}{{tan}^{2}x+1}$=$\frac{4}{5}$,
cos2x=$\frac{{cos}^{2}x-s{in}^{2}x}{{sin}^{2}x+{cos}^{2}x}$=$\frac{1-{tan}^{2}x}{{tan}^{2}x+1}$=-$\frac{3}{5}$.
∴f(α)=$\frac{1}{2}$$(sin2x+cos2x)+\frac{1}{2}$=$\frac{3}{5}$.
(2)sinθ,cosθ是方程x2-ax+a=0的两根,sinθ+cosθ=a,sinθcosθ=a,
∴a2-2a=1,解得$a=1±\sqrt{2}$,
又$\left|sinθcosθ\right|≤\frac{1}{2}$,
∴a=$1-\sqrt{2}$$sinθcosθ=1-\sqrt{2}$,
f(θ)-$\frac{1}{2}cos2θ-\frac{1}{2}$=1$-\sqrt{2}$.
点评 本题考查三角函数的恒等变换,同角三角函数的基本关系式以及诱导公式,两角和与差的三角函数,考查计算能力.

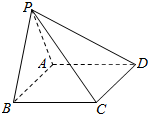 如图,在四棱锥P-ABCD中,底面ABCD是正方形.已知AP=PB=AD=2,PD=2$\sqrt{2}$.
如图,在四棱锥P-ABCD中,底面ABCD是正方形.已知AP=PB=AD=2,PD=2$\sqrt{2}$.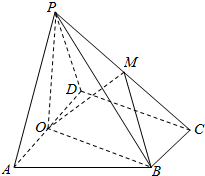 如图,在四棱锥P-ABCD中,底面ABCD为直角梯形,AD∥BC,∠ADC=90°,平面PAD⊥底面ABCD,O为AD的中点,PA=PD=2,BC=$\frac{1}{2}$AD=1,CD=$\sqrt{3}$,M是棱PC上一点,PA∥平面MOB;
如图,在四棱锥P-ABCD中,底面ABCD为直角梯形,AD∥BC,∠ADC=90°,平面PAD⊥底面ABCD,O为AD的中点,PA=PD=2,BC=$\frac{1}{2}$AD=1,CD=$\sqrt{3}$,M是棱PC上一点,PA∥平面MOB; 
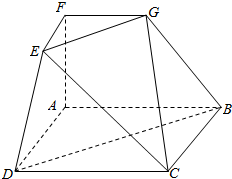 如图,在几何体ABCD-EFG中,下地面ABCD为正方形,上底面EFG为等腰直角三角形,其中EF⊥FG,且EF∥AD,FG∥AB,AF⊥面ABCD,AB=2FG=2,BE=BD,M是DE的中点.
如图,在几何体ABCD-EFG中,下地面ABCD为正方形,上底面EFG为等腰直角三角形,其中EF⊥FG,且EF∥AD,FG∥AB,AF⊥面ABCD,AB=2FG=2,BE=BD,M是DE的中点. 64个正数排成8行8列,如图所示:在符号aij(1≤i≤8,1≤j≤8)中,i表示该数所在行数,j表示该数所在列数,已知每一行都成等差数列,而每一列都成等比数列(且每列公比都相等)若a11=$\frac{1}{2}$,a24=1,a32=$\frac{1}{4}$,则aij=$\frac{j}{{2}^{i}}$.
64个正数排成8行8列,如图所示:在符号aij(1≤i≤8,1≤j≤8)中,i表示该数所在行数,j表示该数所在列数,已知每一行都成等差数列,而每一列都成等比数列(且每列公比都相等)若a11=$\frac{1}{2}$,a24=1,a32=$\frac{1}{4}$,则aij=$\frac{j}{{2}^{i}}$.