题目内容
若关于x的方程( )x=
)x= 有负实数解,则实数a的取值范围为 .
有负实数解,则实数a的取值范围为 .
【答案】分析:利用指数函数的底数大于0小于1时,函数递减把( )x=
)x=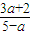 有负实数解转化为
有负实数解转化为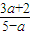 >1,求出a的取值范围.
>1,求出a的取值范围.
解答:解:∵x<0时,y=( )x>1
)x>1
∴x的方程( )x=
)x=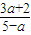 有负实数解转化为
有负实数解转化为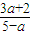 >1⇒
>1⇒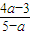 >0⇒(4a-3)(a-5)<0⇒
>0⇒(4a-3)(a-5)<0⇒ <a<5
<a<5
故答案为: <a<5.
<a<5.
点评:本题考查了指数函数的性质.当指数函数的底数大于0小于1时,函数递减且过(0,1)点.
 )x=
)x=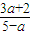 有负实数解转化为
有负实数解转化为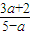 >1,求出a的取值范围.
>1,求出a的取值范围.解答:解:∵x<0时,y=(
 )x>1
)x>1∴x的方程(
 )x=
)x=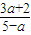 有负实数解转化为
有负实数解转化为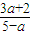 >1⇒
>1⇒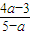 >0⇒(4a-3)(a-5)<0⇒
>0⇒(4a-3)(a-5)<0⇒ <a<5
<a<5故答案为:
 <a<5.
<a<5.点评:本题考查了指数函数的性质.当指数函数的底数大于0小于1时,函数递减且过(0,1)点.

练习册系列答案
 黄冈创优卷系列答案
黄冈创优卷系列答案
相关题目
