题目内容
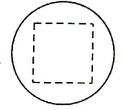
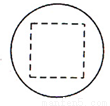
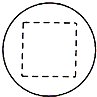
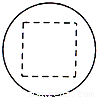 已知某一多面体内接于球构成一个简单组合体,如果该组合体的正视图、俯视图、均如图所示,且图中的四边形是边长为2的正方形,则该球的表面积是 .
已知某一多面体内接于球构成一个简单组合体,如果该组合体的正视图、俯视图、均如图所示,且图中的四边形是边长为2的正方形,则该球的表面积是 .
【答案】分析:由三视图可知,组合体是球内接正方体,正方体的棱长为2,求出球的半径,然后求出球的表面积即可.
解答:解:由三视图可知,组合体是球内接正方体,正方体的棱长为2,
球的直径就是正方体的体对角线的长,所以2r=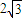 ,r=
,r=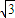 ,
,
所以球的表面积为:4πr2=12π.
故答案为:12π.
点评:本题考查三视图与几何体的关系,球的内接体以及球的表面积的求法,考查空间想象能力与计算能力.
解答:解:由三视图可知,组合体是球内接正方体,正方体的棱长为2,
球的直径就是正方体的体对角线的长,所以2r=
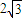 ,r=
,r=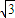 ,
,所以球的表面积为:4πr2=12π.
故答案为:12π.
点评:本题考查三视图与几何体的关系,球的内接体以及球的表面积的求法,考查空间想象能力与计算能力.

练习册系列答案
相关题目
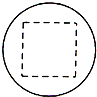 (2013•福建)已知某一多面体内接于球构成一个简单组合体,如果该组合体的正视图、俯视图、均如图所示,且图中的四边形是边长为2的正方形,则该球的表面积是
(2013•福建)已知某一多面体内接于球构成一个简单组合体,如果该组合体的正视图、俯视图、均如图所示,且图中的四边形是边长为2的正方形,则该球的表面积是