题目内容

15．已知数列{an}满足$\frac{ln{a}_{1}}{2}$•$\frac{ln{a}_{2}}{5}$•$\frac{ln{a}_{3}}{8}$•…•$\frac{ln{a}_{n}}{3n-1}$=$\frac{3n+2}{2}$（n∈N*），则a10=（　　）
A．e26B．e29C．e32D．e35

分析 利用已知条件，得到通项公式，然后求解a10．

解答 解：数列{an}满足$\frac{ln{a}_{1}}{2}$•$\frac{ln{a}_{2}}{5}$•$\frac{ln{a}_{3}}{8}$•…•$\frac{ln{a}_{n}}{3n-1}$=$\frac{3n+2}{2}$（n∈N*），
可知$\frac{ln{a}_{1}}{2}$•$\frac{ln{a}_{2}}{5}$•$\frac{ln{a}_{3}}{8}$•…•$\frac{ln{a}_{n-1}}{3n-4}$=$\frac{3n-1}{2}$，
两式作商可得：$\frac{ln{a}_{n}}{3n-1}$=$\frac{\frac{3n+2}{2}}{\frac{3n-1}{2}}$=$\frac{3n+2}{3n-1}$，
可得lnan=3n+2．
a10=e32．
故选：C．

点评 本题考查数列递推关系式的应用，数列的通项公式的求法，考查计算能力．

练习册系列答案
相关题目
19．已知数列{an}是一个无穷等比数列，公比为q．
（1）将数列{an}中的前k项去掉，剩余各项组成一个新的数列，这个新数列是等比数列吗？如果是，它的首项与公比分别是多少？
（2）取出数列{an}中的所有奇数项，组成一个新的数列，这个新数列是等比数列吗？如果是，它的首项与公比分别是多少？
（3）在数列{an}中，每隔10项取出一项，组成一个新的数列，这个新数列是等比数列吗？如果是，它的公比是多少？你能根据得到的结论作出一个猜想吗？
6．已知f（x）是定义在R上不恒为零的函数，对于任意的x，y∈R，都有f（x•y）=xf（y）+yf（x）成立．数列{an}满足an=f（2n）（n∈N+），且a1=2．
（1）试求数列{an}的通项公式an．
（2）若bn=$\frac{{a}_{n}}{n（n+1）^{2}}$，求数列{bn}的最小项．
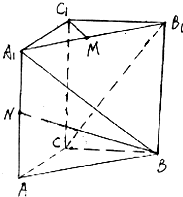3．如图，直三棱柱ABC-A1B1C1，底面△ABC中，CA=CB=2，AB=2$\sqrt{2}$，棱AA1=4，M，N分别是A1B1，AA1的中点．
（1）求$\overrightarrow{{A_1}B}$•$\overrightarrow{{C_1}B}$的值；
（2）求直线BN与平面AB1C所成的角的正弦值．
10．设函数f（x）=x3-3ax2+3（2-a）x，a∈R．
（Ⅰ）求f（x）的单调递增区间；
（Ⅱ）若y=f（x）的图象与x轴相切于原点，当0＜x2＜x1，f（x1）=f（x2），求证：x1+x2＜8．
20．求定积分 ${∫}_{0}^{\frac{1}{2}}（1+x）^{n}dx$=$\frac{1}{n+1}[（\frac{3}{2}）^{n+1}-1]$．
7．若角α是第一象限角，则-α，2α，$\frac{α}{3}$分别在哪个区域？
4．设数列{an}的通项公式an=$\frac{n}{n+3}$，则比较an与an-1的大小关系．
5．已知$\overrightarrow{a}$是非零向量，且$\overrightarrow{b}$≠$\overrightarrow{c}$，求证：$\overrightarrow{a}$•$\overrightarrow{b}$=$\overrightarrow{a}$•$\overrightarrow{c}$=?$\overrightarrow{a}$⊥（$\overrightarrow{b}$-$\overrightarrow{c}$）．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网