题目内容
(本小题满分12分)
已知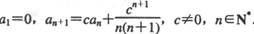 .
.
(I )求数列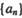 丨的通项:
丨的通项:
(II)若对任意, ?
?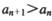 恒成立,求c的取值范围.
恒成立,求c的取值范围.
已知
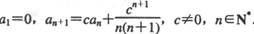 .
.(I )求数列
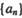 丨的通项:
丨的通项:(II)若对任意,
 ?
?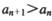 恒成立,求c的取值范围.
恒成立,求c的取值范围.(Ⅰ)∵an+1=can+,∴=+,-=-.
∴=+(-)+(-)+…+(-)
=0+1-+-+…+-=1-,
∴an=cn.………………………………………………………………………6分
(Ⅱ)an+1>an即cn+1>cn.
当c<0时,上面不等式显然不恒成立;
当c>0时,上面不等式等价于c>=1-.………………………………9分
1-是n的增函数,(1-)=1,
∴c≥1.
综上,c的取值范围是.…………………12分
∴=+(-)+(-)+…+(-)
=0+1-+-+…+-=1-,
∴an=cn.………………………………………………………………………6分
(Ⅱ)an+1>an即cn+1>cn.
当c<0时,上面不等式显然不恒成立;
当c>0时,上面不等式等价于c>=1-.………………………………9分
1-是n的增函数,(1-)=1,
∴c≥1.
综上,c的取值范围是.…………………12分
略

练习册系列答案
 新思维寒假作业系列答案
新思维寒假作业系列答案
相关题目
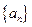 满足
满足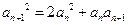 , 且
, 且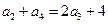 ,
,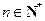 .
. 数列
数列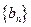 的前
的前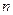 项和为
项和为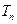 ,令
,令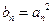 ,其中
,其中 ,试比较
,试比较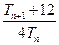 与
与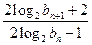 的大小,并加以证明.
的大小,并加以证明.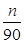 (21n-n2-5)(n=1,2,……,12),按此预测,在本年度内,
(21n-n2-5)(n=1,2,……,12),按此预测,在本年度内,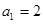 ,点
,点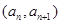
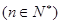 在函数
在函数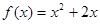 的图象上,设
的图象上,设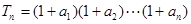 ,
,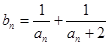 ,数列
,数列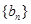 的前
的前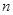 项为
项为 。
。 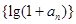 是等比数列;(2)求
是等比数列;(2)求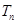 及数列
及数列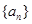 的通项;
的通项;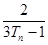 =1
=1
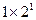 ,
,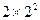 ,
,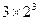 ,…,的前
,…,的前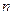 项之和为
项之和为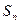 ,则
,则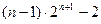
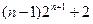
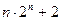
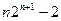
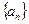 的前n项和为
的前n项和为 则数列的通项公式
则数列的通项公式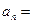 _____
_____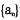 满足:
满足: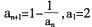 ,记数列
,记数列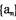 的前n项之积为
的前n项之积为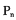 ,则
,则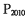 =___
=___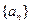 的前n项和
的前n项和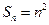 ,则
,则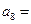 ( )
( )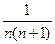 (n∈N*),若前n项的和为
(n∈N*),若前n项的和为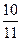 ,则项数为
,则项数为