题目内容
过原点与曲线 相切的切线方程为
相切的切线方程为
- A.
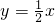
- B.y=2x
- C.y=x
- D.

A
分析:先设切点坐标为P,然后根据导数的几何意义在x=a处的导数即为切线的斜率,以及根据原点和p点求出斜率k,解方程即可求出切点,再根据点斜时求出切线方程即可.
解答:设切点P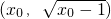 ,那么切线斜率,
,那么切线斜率,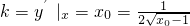 ,
,
又因为切线过点O(0,0)及点P
则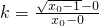 ,∴
,∴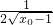 =
=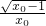 ,
,
解得x0=2,∴ ,从而切线方程为
,从而切线方程为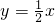 ,
,
故选A
点评:本题主要考查了利用导数研究曲线上某点切线方程,以及切线过某点的问题,常常利用导数的几何意义进行求解,属于基础题.
分析:先设切点坐标为P,然后根据导数的几何意义在x=a处的导数即为切线的斜率,以及根据原点和p点求出斜率k,解方程即可求出切点,再根据点斜时求出切线方程即可.
解答:设切点P
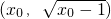 ,那么切线斜率,
,那么切线斜率,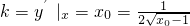 ,
,又因为切线过点O(0,0)及点P
则
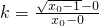 ,∴
,∴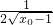 =
=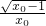 ,
,解得x0=2,∴
 ,从而切线方程为
,从而切线方程为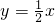 ,
,故选A
点评:本题主要考查了利用导数研究曲线上某点切线方程,以及切线过某点的问题,常常利用导数的几何意义进行求解,属于基础题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目