Question

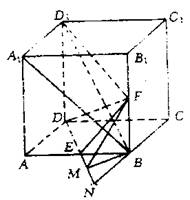
（08年石室中学）正方体ABCD―A₁B₁C₁D₁中，E、F分别为AB与BB₁的中点。

   （I）求证：EF⊥平面A₁D₁B；

   （II）求二面角F―DE―C的正切值；

   （III）若AA₁=2，求三棱锥D₁―DEF的体积。

 

 

 

 

Answer 1

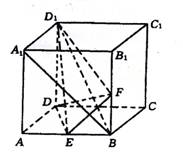
解析:方法一：（I）∵E、F分别为AB与BB₁的中点

∴EF∥AB₁，而AB₁⊥A₁B，∴EF⊥A₁B

又D₁A₁⊥平面ABB₁A₁，∴D₁A₁⊥EF，∴EF⊥平面AD₁B₁        …………2分

   （II）设CB交DE的延长线于点N，作BM⊥DN于M点，连FM

∵FB⊥平面ABCD，∴FM⊥DN，

∴∠FMB为二面角F―DE―C的平面角                                  …………5分

设正方体棱长为a，则中，

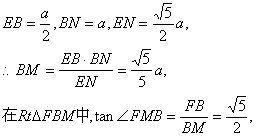
∴二面角F―DE―C的正切值为                                      …………8分

   （III）连结DB，∵BB₁∥DD₁

                                                             …………12分

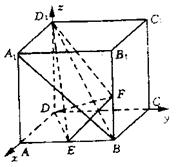
方法二：如图所示，分别以DA、DC、DD₁为x轴、y轴、z轴建立空间直角坐标系

D―ACD₁，不妨令正方体的棱长为2。

   （I）∵E、F分别为AB与BB₁的中点

∴E（2，1，0），F（2，2，1），A₁（2，0，2）

D₁（0，0，2），B（2，2，0），

，

，…………2分

，

   （II）显然，平面DEC的法向量为

解得                                                                   …………6分

记二面角F―DE―C的平面角为α，

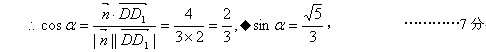
故二面角F―DE―C的正切值◆              …………8分