题目内容
如图,有一直角墙角,两边的长度足够长,在P处有一棵树与两墙的距离分别
是 、4m,不考虑树的粗细,现在用16m长的篱笆, 借助墙角围成一个矩形的共圃ABCD,设此矩形花圃的面积为Sm2,S的最大值为
、4m,不考虑树的粗细,现在用16m长的篱笆, 借助墙角围成一个矩形的共圃ABCD,设此矩形花圃的面积为Sm2,S的最大值为 ,若将这棵树围在花圃中,则函数
,若将这棵树围在花圃中,则函数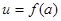 的图象大致是( )
的图象大致是( )

C
解析试题分析:假设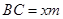 则
则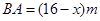 .所以
.所以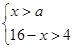 即
即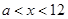 .花圃的面积为
.花圃的面积为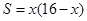 (
(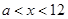 ).所以
).所以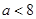 时,
时,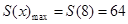 .当
.当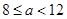 时,
时,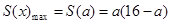 ,这一段的图像是递减的,故选C.
,这一段的图像是递减的,故选C.
考点:1.阅读理解清题意.2.二次函数的最值问题.3.含参数的最值的求法.

练习册系列答案
相关题目
已知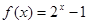 ,
, ,规定:当
,规定:当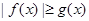 时,
时, 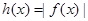 ;当
;当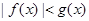 时,
时,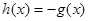 ,则
,则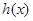 ( )
( )
A.有最小值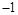 ,最大值1 ,最大值1 | B.有最大值1,无最小值 |
C.有最小值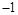 ,无最大值 ,无最大值 | D.有最大值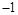 ,无最小值 ,无最小值 |
已知函数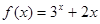 的零点所在的一个区间是( )
的零点所在的一个区间是( )
| A.(-2,-1) | B.(-1,0) | C.(0,1) | D.(1,2) |
设函数f(x)=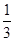 x-ln x(x>0),则y=f(x)( ).
x-ln x(x>0),则y=f(x)( ).
A.在区间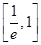 ,(1,e)内均有零点 ,(1,e)内均有零点 |
B.在区间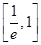 ,(1,e)内均无零点 ,(1,e)内均无零点 |
C.在区间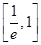 内有零点,在区间(1,e)内无零点 内有零点,在区间(1,e)内无零点 |
D.在区间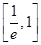 内无零点,在区间(1,e)内有零点 内无零点,在区间(1,e)内有零点 |
已知函数y=f(x-1)的图象关于直线x=1对称,且当x∈(-∞,0),f(x)+xf′(x)<0成立,若a=(20.2)·f(20.2),b=(ln 2)·f(ln 2),c= ·f
·f ,则a,b,c的大小关系是( ).
,则a,b,c的大小关系是( ).
| A.a>b>c | B.b>a>c |
| C.c>a>b | D.a>c>b |
 的图像的大致形状是( )
的图像的大致形状是( )

 上的值域为 ( ).
上的值域为 ( ).