题目内容
已知抛物线 上任意一点到焦点F的距离比到
上任意一点到焦点F的距离比到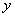 轴的距离大1,
轴的距离大1,
(1)求抛物线C的方程;
(2)过焦点F的直线与抛物线 交于A、B两点,求
交于A、B两点,求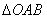 面积的最小值。
面积的最小值。
(3)过点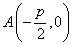 的直线交抛物线
的直线交抛物线 于P、Q两点,设点P关于
于P、Q两点,设点P关于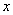 轴的对称点为R,求证:直线RQ必过定点.
轴的对称点为R,求证:直线RQ必过定点.
【答案】
解析:(1)设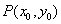 为抛物线
为抛物线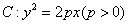 上一点,作
上一点,作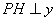 轴,垂足为H,连接PF,因
轴,垂足为H,连接PF,因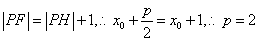 ,所求抛物线C的方程为
,所求抛物线C的方程为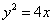 ;------------4分
;------------4分
(2)由(1)可得焦点坐标为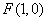 ,易得:当斜率不存在时,取最小值分
,易得:当斜率不存在时,取最小值分
(3)因A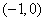 ,设
,设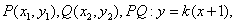 与
与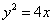 联立得
联立得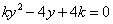 ,
,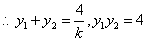 ,又因点P关于
,又因点P关于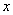 轴的对称点为R,则
轴的对称点为R,则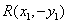 ,
,
因此直线RQ的方程为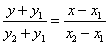 ,
,
即有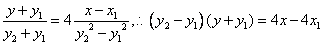 ,
,
因此有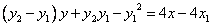 ,因
,因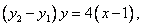
所以直线RQ必过定点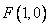 .
------------15分
.
------------15分

练习册系列答案
相关题目
 上任意一点
上任意一点 到直线
到直线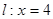 的距离是它到点
的距离是它到点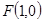 距离的
距离的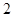 倍;曲线
倍;曲线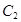 是以原点为顶点,
是以原点为顶点,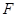 为焦点的抛物线.
为焦点的抛物线.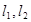 ,其中
,其中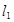 与
与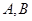 ,
,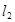 与
与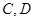 ,求四边形
,求四边形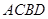 面积的取值范围.
面积的取值范围.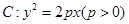 上任意一点到焦点F的距离比到
上任意一点到焦点F的距离比到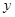 轴的距离大1,(1)求抛物线C的方程;(2)若过焦点F的直线交抛物线于M,N两点,M在第一象限,且
轴的距离大1,(1)求抛物线C的方程;(2)若过焦点F的直线交抛物线于M,N两点,M在第一象限,且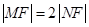 ,求直线MN的方程;(3)过点
,求直线MN的方程;(3)过点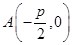 的直线交抛物线
的直线交抛物线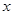 轴的对称点为R,求证:直线RQ必过定点.
轴的对称点为R,求证:直线RQ必过定点.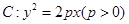 上任意一点到焦点F的距离比到
上任意一点到焦点F的距离比到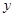 轴的距离大1,(1)求抛物线C的方程;(2)若过焦点F的直线交抛物线于M,N两点,M在第一象限,且
轴的距离大1,(1)求抛物线C的方程;(2)若过焦点F的直线交抛物线于M,N两点,M在第一象限,且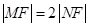 ,求直线MN的方程;(3)过点
,求直线MN的方程;(3)过点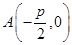 的直线交抛物线
的直线交抛物线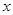 轴的对称点为R,求证:直线RQ必过定点.
轴的对称点为R,求证:直线RQ必过定点.