题目内容
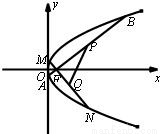
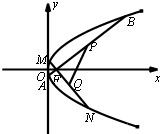 已知动点M到点F(1,0)的距离,等于它到直线x=-1的距离.
已知动点M到点F(1,0)的距离,等于它到直线x=-1的距离.(Ⅰ)求点M的轨迹C的方程;
(Ⅱ)过点F任意作互相垂直的两条直线l1,l2,分别交曲线C于点A,B和M,N.设线段AB,MN的中点分别为P,Q,求证:直线PQ恒过一个定点;
(Ⅲ)在(Ⅱ)的条件下,求△FPQ面积的最小值.
分析:(Ⅰ)设动点M的坐标为(x,y),由题意得
=|x+1|,由此能求出点M的轨迹C的方程.
(Ⅱ)设A,B两点坐标分别为(x1,y1),(x2,y2),则点P的坐标为(
,
).由题意可设直线l1的方程为y=k(x-1)(k≠0),由
得k2x2-(2k2+4)x+k2=0.再由根的判别式和根与系数的关系进行求解.
(Ⅲ)题题设能求出|EF|=2,所以△FPQ面积S=
|FE|(
+2|k|)=2(
+|k|)≥4.
| (x-1)2+y2 |
(Ⅱ)设A,B两点坐标分别为(x1,y1),(x2,y2),则点P的坐标为(
| x1+x2 |
| 2 |
| y1+y2 |
| 2 |
|
(Ⅲ)题题设能求出|EF|=2,所以△FPQ面积S=
| 1 |
| 2 |
| 2 |
| |k| |
| 1 |
| |k| |
解答:解:(Ⅰ)设动点M的坐标为(x,y),
由题意得,
=|x+1|,
化简得y2=4x,
所以点M的轨迹C的方程为y2=4x.(4分)
(Ⅱ)设A,B两点坐标分别为(x1,y1),(x2,y2),
则点P的坐标为(
,
).
由题意可设直线l1的方程为y=k(x-1)(k≠0),
由
得k2x2-(2k2+4)x+k2=0.
△=(2k2+4)2-4k4=16k2+16>0.
因为直线l1与曲线C于A,B两点,
所以x1+x2=2+
,
y1+y2=k(x1+x2-2)=
.
所以点P的坐标为(1+
,
).
由题知,直线l2的斜率为-
,同理可得点的坐标为(1+2k2,-2k).
当k≠±1时,有1+
≠1+2k2,
此时直线PQ的斜率kPQ=
=
.
所以,直线PQ的方程为y+2k=
(x-1-2k2),
整理得yk2+(x-3)k-y=0.
于是,直线PQ恒过定点E(3,0);
当k=±1时,直线PQ的方程为x=3,也过点E(3,0).
综上所述,直线PQ恒过定点E(3,0).(10分)
(Ⅲ)可求得|EF|=2,
所以△FPQ面积S=
|EF|(
+2|k|)=2(
+|k|)≥4.
当且仅当k=±1时,“=”成立,所以△FPQ面积的最小值为4.(13分)
由题意得,
| (x-1)2+y2 |
化简得y2=4x,
所以点M的轨迹C的方程为y2=4x.(4分)
(Ⅱ)设A,B两点坐标分别为(x1,y1),(x2,y2),
则点P的坐标为(
| x1+x2 |
| 2 |
| y1+y2 |
| 2 |
由题意可设直线l1的方程为y=k(x-1)(k≠0),
由
|
△=(2k2+4)2-4k4=16k2+16>0.
因为直线l1与曲线C于A,B两点,
所以x1+x2=2+
| 4 |
| k2 |
y1+y2=k(x1+x2-2)=
| 4 |
| k |
所以点P的坐标为(1+
| 2 |
| k2 |
| 2 |
| k |
由题知,直线l2的斜率为-
| 1 |
| k |
当k≠±1时,有1+
| 2 |
| k2 |
此时直线PQ的斜率kPQ=
| ||
1+
|
| k |
| 1-k2 |
所以,直线PQ的方程为y+2k=
| k |
| 1-k2 |
整理得yk2+(x-3)k-y=0.
于是,直线PQ恒过定点E(3,0);
当k=±1时,直线PQ的方程为x=3,也过点E(3,0).
综上所述,直线PQ恒过定点E(3,0).(10分)
(Ⅲ)可求得|EF|=2,
所以△FPQ面积S=
| 1 |
| 2 |
| 2 |
| |k| |
| 1 |
| |k| |
当且仅当k=±1时,“=”成立,所以△FPQ面积的最小值为4.(13分)
点评:本题考查圆锥曲线和直线的位置关系和综合应用,具有一定的难度,解题时要认真审题,注意挖掘隐含条件,仔细解答.

练习册系列答案
相关题目
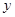 轴的距离大1个单位长度。
轴的距离大1个单位长度。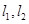 ,分别交曲线C于点A、B和M、N,设线段AB、MN的中点分别为P、Q,求证:直线PQ恒过一个定点。
,分别交曲线C于点A、B和M、N,设线段AB、MN的中点分别为P、Q,求证:直线PQ恒过一个定点。