题目内容
在等比数列中,前n项和为Sn,已知S4=2,S8=8,求S12.
思路解析:若把给定条件都用a1,q表示,通过解方程组可以求得,这是基本方法.但注意到S4,S8,S12是有规律的,可以考虑用等比数列的性质来解. 解法一:设等比数列的公比为q, 若q=1,则S4=4a1=2,∴a1= S8=8a1=8,a1=1. 这是相互矛盾的,因此q≠1. ∴S4= ∴q4=3. 而 ∴S12=26. 解法二:在等比数列中,S4,S8-S4,S12-S8仍然成等比数列,即2,6,S12-8成等比数列. ∴2(S12-8)=62. 解得S12=26. 深化升华 (1)应用等比数列的前n项和公式一定要先验证公比q是否可以是1,然后再选择公式. (2)由Sn= (3)在等比数列中,Sn,S2n-Sn,S3n-S2n仍成等比数列,其公比为qn. 在应用此性质时,注意不是Sn,S2n,S3n成等比数列.![]() .
.![]() ,S8=
,S8= ![]() .
.![]() 1+q4=4.
1+q4=4.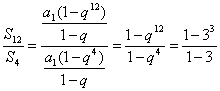 =13.
=13.![]() (1-qn)可以看出,
(1-qn)可以看出,![]() 是常数,Sn仅随qn变化.因此,在解法一中,不必求出
是常数,Sn仅随qn变化.因此,在解法一中,不必求出![]() 的值,只需通过S4,S8的比值来求得q,然后求得S12.
的值,只需通过S4,S8的比值来求得q,然后求得S12.

黄冈海淀大考卷单元期末冲刺100分系列答案

课堂新动态系列答案

初中历史与社会思想品德精讲精练系列答案

高效练习系列答案
训练与检测完全试卷系列答案
每课一练(福建)系列答案
在等比数列 中,前n项和为
中,前n项和为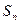 ,若
,若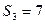 ,
,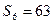 ,则公比
,则公比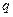 的值是 ( )
的值是 ( )
| A.2 | B.-2 | C.3 | D.-3 |
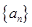 中,前n项和为
中,前n项和为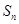 ,若
,若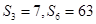 ,则公比
,则公比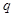 的值为 .
的值为 . 中,前n项和为
中,前n项和为 ,若
,若 ,
, ,则公比
,则公比 的值是 ( )
的值是 ( )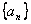 中,前n项和为
中,前n项和为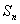 ,若
,若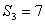 ,
,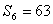 ,则公比
,则公比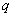 的值是 ( )
的值是 ( )