题目内容
若等比数列的前n项和是48,前2n项和是60,则前3n项的和是( )A.183 B.108 C.75 D.63
解法一:Sn=![]() =48,
=48,
S2n=![]() =
=![]() =Sn(1+qn),
=Sn(1+qn),
∴60=48(1+qn),得qn=![]() .
.
∴S3n=![]() =Sn(1+qn+q2n)=63.
=Sn(1+qn+q2n)=63.
解法二:Sn、S2n-Sn、S3n-S2n成等比数列,从而有Sn=48,S2n-Sn=12,S3n-S2n=3,
∴S3n=63.
解法三:令n=1,S1=a1=48,S2n=S2=a1+a2=48+a2=60,
∴a2=12,a3=a2·q=12×![]() =3.
=3.
∴S3n=a1+a2+a3=48+12+3=63.
答案:D

练习册系列答案
 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案
相关题目
 的前n项和
的前n项和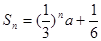 ,则
,则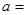 .
.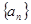 的前n项和为
的前n项和为 S
S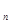 ,a
,a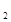 =
6,S
=
6,S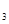 =
21,则公比q=
=
21,则公比q=  的前n项和为
的前n项和为 ,
, ,
, ,则公比q=__________.
,则公比q=__________.