题目内容
11.已知椭圆C的两个焦点分别为F1(-2,0),F2(2,0),且椭圆C经过点(-2,3).(1)求椭圆C的方程;
(2)求椭圆C内接矩形面积的最大值及此时矩形的周长.
分析 (1)通过椭圆焦点坐标可知c=2,利用两点间距离公式及椭圆定义可知a=4,进而可得结论;
(2)通过设椭圆C内接矩形位于第一象限的顶点坐标为(x0,y0)(x0>0,y0>0),根据椭圆的对称性及基本不等式可知椭圆C的内接矩形的面积的最大值,进而计算可得周长.
解答 解:(1)由椭圆焦点坐标可知c=2,
∵椭圆C经过点(-2,3),
∴由椭圆定义可知2a=$\sqrt{[-2-(-2)]^{2}+(0-3)^{2}}$+$\sqrt{[2-(-2)]^{2}+(0-3)^{2}}$=8,即a=4,
∴b2=a2-c2=12,
∴椭圆C的方程为:$\frac{{x}^{2}}{16}+\frac{{y}^{2}}{12}=1$;
(2)根据椭圆的对称性,椭圆C内接矩形的对称轴必为坐标轴,
设椭圆C内接矩形位于第一象限的顶点坐标为(x0,y0)(x0>0,y0>0),
记椭圆C的内接矩形的面积为S,
∵$\frac{{{x}_{0}}^{2}}{16}+\frac{{{y}_{0}}^{2}}{12}=1$,
∴S=4x0y0=16$\sqrt{3}$•2•$\frac{{x}_{0}}{4}$•$\frac{{y}_{0}}{2\sqrt{3}}$≤16$\sqrt{3}$•[$(\frac{{x}_{0}}{4})^{2}$+$(\frac{{y}_{0}}{2\sqrt{3}})^{2}$]=$16\sqrt{3}$,
∴椭圆C的内接矩形面积的最大值为$16\sqrt{3}$,
此时$\frac{{x}_{0}}{4}$=$\frac{{y}_{0}}{2\sqrt{3}}$=$\frac{1}{\sqrt{2}}$,解得:x0=$2\sqrt{2}$,y0=$\sqrt{6}$,
∴矩形的周长为4(x0+y0)=$8\sqrt{2}+4\sqrt{6}$.
点评 本题考查椭圆的简单性质,涉及面积、周长公式,利用基本不等式是解决本题的关键,注意解题方法的积累,属于中档题.

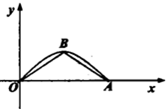 如图是函数f(x)=sinx(x∈[0,π])的图象,其中B为顶点,若在f(x)的图象与x轴所围成的区域内任意投进一个点P,则点P落在△OAB内的概率为( )
如图是函数f(x)=sinx(x∈[0,π])的图象,其中B为顶点,若在f(x)的图象与x轴所围成的区域内任意投进一个点P,则点P落在△OAB内的概率为( )| A. | $\frac{π}{4}$ | B. | $\frac{π}{2}$ | C. | $\frac{1}{4}$ | D. | $\frac{1}{2}$ |