题目内容
在ΔABC中,角A,B,C所对的对边长分别为a、b、c,sinA、sinB、sinC成等比数列,且c= 2a,则cosB的值为
A.  B.
B. 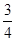 C.
C. 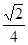 D.
D. 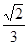
B
解析试题分析:根据题意可知sinA、sinB、sinC成等比数列,因此可知 由正弦定理可知化角为边得到
由正弦定理可知化角为边得到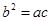 ,结合余弦定理可知
,结合余弦定理可知 ,且c=2a,则可知
,且c=2a,则可知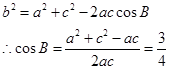
,故选B.
考点:本试题考查了解三角形的知识点。
点评:解决该试题的关键是能利用边角的关系,结合正弦定理和余弦定理来求解得到。熟练的运用两个定理,并能灵活的选择定理来解答,是要结合题目中的条件来确定的,余弦定理适合解决两边及其夹角,和三边的问题来求解三角形,属于中档题。

练习册系列答案
 小学生10分钟口算测试100分系列答案
小学生10分钟口算测试100分系列答案
相关题目
在各项都为正数的等比数列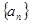 中,首项
中,首项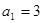 ,前三项和为21,则
,前三项和为21,则 =( )
=( )
| A.33 | B.72 | C.84 | D.189 |
已知等比数列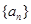 满足
满足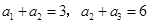 ,则
,则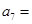 ( )
( )
| A.64 | B.81 | C.128 | D.243 |
在正项等比数列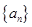 中,已知
中,已知 ,则
,则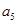 的值为( )
的值为( )
| A.8 | B.6 | C.4 | D.2 |
设等比数列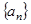 中,前n项和为
中,前n项和为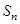 ,已知
,已知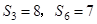 ,则
,则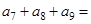
A. | B.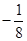 | C.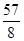 | D.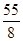 |
在等比数列{an}中,若a1a2a3=2,a2a3a4=16,则公比q= ( )
A. | B.2 | C.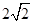 | D.8 |
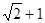 与
与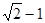 ,两数的等比中项是( )
,两数的等比中项是( )
A.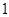 | B.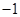 | C.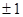 | D.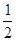 |
等比数列 中,首项
中,首项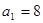 ,公比
,公比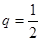 ,那么
,那么 前5项和
前5项和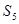 的值是
的值是
A.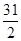 | B.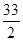 | C.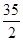 | D.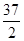 |
 中,每 行 中 的 三 个 数 成 等 差 数 列,且
中,每 行 中 的 三 个 数 成 等 差 数 列,且 、
、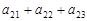 、
、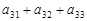 成等比数列,下列四个判断正确的有 (A )
成等比数列,下列四个判断正确的有 (A )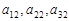 必成等比数列 ②第1列
必成等比数列 ②第1列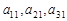 不一定成等比数列
不一定成等比数列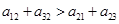 ④若9个数之和等于9,则
④若9个数之和等于9,则