题目内容
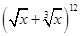 的展开式中有理项共有 项.
的展开式中有理项共有 项.3
试题分析:∵
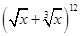 展开式的通项为
展开式的通项为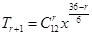 ,其中r=0,1,2,3,4,5,6,7,8,9,10,11,12,有理项中x的次幂为整数,故r=0,6,12,故
,其中r=0,1,2,3,4,5,6,7,8,9,10,11,12,有理项中x的次幂为整数,故r=0,6,12,故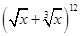 的展开式中有理项共有3项
的展开式中有理项共有3项点评:掌握二项式定理能正确运用二项展开式;能正确写出通项公式,并用通项公式解决有关问题

练习册系列答案
相关题目
题目内容
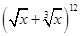 的展开式中有理项共有 项.
的展开式中有理项共有 项.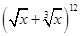 展开式的通项为
展开式的通项为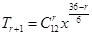 ,其中r=0,1,2,3,4,5,6,7,8,9,10,11,12,有理项中x的次幂为整数,故r=0,6,12,故
,其中r=0,1,2,3,4,5,6,7,8,9,10,11,12,有理项中x的次幂为整数,故r=0,6,12,故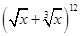 的展开式中有理项共有3项
的展开式中有理项共有3项