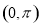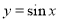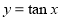题目内容
已知函数 ,
, .
.
(1)若函数 在
在 上不具有单调性,求实数
上不具有单调性,求实数 的取值范围;
的取值范围;
(2)若 .
.
(ⅰ)求实数 的值;
的值;
(ⅱ)设 ,
, ,
, ,当
,当 时,试比较
时,试比较 ,
, ,
, 的大小.
的大小.
(1)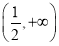 (2)(ⅰ)2(ⅱ)
(2)(ⅰ)2(ⅱ)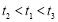
【解析】
试题分析:将二次函数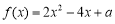 的解析式进行配方,根据其开口方向的对称轴得到该函数的单调区间, 函数
的解析式进行配方,根据其开口方向的对称轴得到该函数的单调区间, 函数 在
在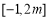 上不具有单调性,说明二次函数的对称轴在区间
上不具有单调性,说明二次函数的对称轴在区间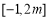 内,由此便可求出的取值范围;
内,由此便可求出的取值范围;
(2)(ⅰ)由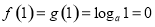 建立方程可解实数
建立方程可解实数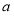 的值;
的值;
(ⅱ)分别根据二次函数、对数函数、指数函数的性质求出当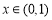 时,
时,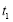 ,
,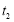 ,
,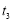 各自的取值范围,进而比较它们的大小.
各自的取值范围,进而比较它们的大小.
试题解析:【解析】
(1)∵抛物线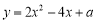 开口向上,对称轴为
开口向上,对称轴为 ,
,
∴函数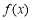 在
在 单调递减,在
单调递减,在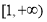 单调递增, 2分
单调递增, 2分
∵函数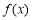 在
在 上不单调
上不单调
∴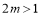 ,得
,得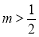 ,
,
∴实数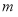 的取值范围为
的取值范围为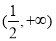 5分
5分
(2)(ⅰ)∵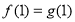 ,
,
∴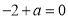
∴实数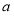 的值为
的值为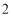 . 8分
. 8分
(ⅱ)∵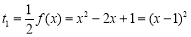 , 9分
, 9分
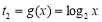 ,
,
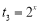 ,
,
∴当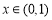 时,
时,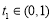 ,
,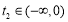 ,
,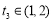 , 12分
, 12分
∴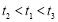 . 13分
. 13分
考点:二次函数、指数函数、对数函数的性质.

练习册系列答案
 快乐5加2金卷系列答案
快乐5加2金卷系列答案
相关题目