题目内容
(1)试讨论方程(1-k)x2+(3-k2)y2=4(k∈R)所表示的曲线;(2)试给出方程
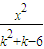 +
+ =1表示双曲线的充要条件.
=1表示双曲线的充要条件.
【答案】分析:(1)分 3-k2 >1-k>0、1-k>3-k2>0、1-k=3-k2>0、(1-k)(3-k2)<0、(1-k)(3-k2)=0这几种情况进行讨论.
(2)方程表示双曲线的充要条件是:(k2+k-6)(6k2-k-1)<0,解不等式求出 k的取值范围.
解答:解:(1)当3-k2>1-k>0,即 k∈(-1,1),方程所表示的曲线是焦点在x轴上的椭圆;
1-k>3-k2>0,即 k∈(- ,-1),方程所表示的曲线是焦点在y轴上的椭圆;
,-1),方程所表示的曲线是焦点在y轴上的椭圆;
1-k=3-k2>0,即 k=-1时,表示的是一个圆;
(1-k)(3-k2)<0⇒k∈(-∞,-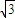 )∪(1,
)∪(1,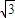 ),表示的是双曲线;
),表示的是双曲线;
k=1,k=-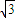 ,表示的是两条平行直线; k=
,表示的是两条平行直线; k=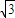 ,表示的图形不存在.
,表示的图形不存在.
(2)由(k2+k-6)(6k2-k-1)<0得 (k+3)(k-2)(3k+1)(2k-1)<0,
即 k∈(-3,- )∪(
)∪( ,2).
,2).
点评:本题考查二元二次方程表示的曲线类型,椭圆、圆、双曲线、直线的方程的特征,体现了分类讨论的数学思想.
(2)方程表示双曲线的充要条件是:(k2+k-6)(6k2-k-1)<0,解不等式求出 k的取值范围.
解答:解:(1)当3-k2>1-k>0,即 k∈(-1,1),方程所表示的曲线是焦点在x轴上的椭圆;
1-k>3-k2>0,即 k∈(-
 ,-1),方程所表示的曲线是焦点在y轴上的椭圆;
,-1),方程所表示的曲线是焦点在y轴上的椭圆;1-k=3-k2>0,即 k=-1时,表示的是一个圆;
(1-k)(3-k2)<0⇒k∈(-∞,-
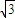 )∪(1,
)∪(1,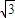 ),表示的是双曲线;
),表示的是双曲线;k=1,k=-
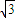 ,表示的是两条平行直线; k=
,表示的是两条平行直线; k=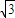 ,表示的图形不存在.
,表示的图形不存在.(2)由(k2+k-6)(6k2-k-1)<0得 (k+3)(k-2)(3k+1)(2k-1)<0,
即 k∈(-3,-
 )∪(
)∪( ,2).
,2).点评:本题考查二元二次方程表示的曲线类型,椭圆、圆、双曲线、直线的方程的特征,体现了分类讨论的数学思想.

练习册系列答案
相关题目
 已知
已知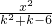 +
+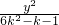 =1表示双曲线的充要条件.
=1表示双曲线的充要条件.