题目内容
设p为常数,函数f(x)=log2(1-x)+plog2(1+x)为奇函数.
(1)求p的值;(2)设f(
)+f(
)=f(x0),求x0的值;
(3)若f(x)>2,求x的取值范围.
(1)求p的值;(2)设f(
| 1 |
| 2 |
| 1 |
| 3 |
(3)若f(x)>2,求x的取值范围.
分析:(1)求出函数的定义域,根据函数是奇函数,f(x)+f(-x)=0对x∈(-1,1)恒成立,可构造关于p的方程,进而求出p的值;
(2)根据(1)可得函数f(x)的解析式,进而根据关于x0的方程,解方程可得x0的值;
(3)根据(1)可得函数f(x)的解析式,构造关于x的不等式,解不等式可得x的取值范围.
(2)根据(1)可得函数f(x)的解析式,进而根据关于x0的方程,解方程可得x0的值;
(3)根据(1)可得函数f(x)的解析式,构造关于x的不等式,解不等式可得x的取值范围.
解答:解:(1)若函数的解析式有意义
,
则函数f(x)的定义域为(-1,1)…(2分)
因为f(x)是奇函数,
所以f(x)+f(-x)=0对x∈(-1,1)恒成立,
log2(1-x)+plog2(1+x)+log2(1+x)+plog2(1-x)=0对x∈(-1,1)恒成立,
即(p+1)[log2(1-x)+log2(1+x)]=0对x∈(-1,1)恒成立,
即(p+1)log2(1-x2)=0对x∈(-1,1)恒成立,
故p+1=0
所以p=-1.…(6分)
(2)由(1)可得f(x)=log2(1-x)-log2(1+x),
则f(
)+f(
)=log2(1-
)-log2(1+
)+log2(1-
)-log2(1+
)
=log2(
)-log2(
)+log2(
)-log2(
)
=log2(
÷
×
÷
)=log2(
)
f(x0)=log2(1-x0)-log2(1+x0)=log2(
),
故
=
解方程得x0=
…(10分)
(3)f(x)=log2(1-x)-log2(1+x),
则f(x)>2等价于
>4,
解得:-1<x<-
,
所以x的取值范围是-1<x<-
.…(14分)
|
则函数f(x)的定义域为(-1,1)…(2分)
因为f(x)是奇函数,
所以f(x)+f(-x)=0对x∈(-1,1)恒成立,
log2(1-x)+plog2(1+x)+log2(1+x)+plog2(1-x)=0对x∈(-1,1)恒成立,
即(p+1)[log2(1-x)+log2(1+x)]=0对x∈(-1,1)恒成立,
即(p+1)log2(1-x2)=0对x∈(-1,1)恒成立,
故p+1=0
所以p=-1.…(6分)
(2)由(1)可得f(x)=log2(1-x)-log2(1+x),
则f(
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 3 |
=log2(
| 1 |
| 2 |
| 3 |
| 2 |
| 2 |
| 3 |
| 4 |
| 3 |
=log2(
| 1 |
| 2 |
| 3 |
| 2 |
| 2 |
| 3 |
| 4 |
| 3 |
| 1 |
| 6 |
f(x0)=log2(1-x0)-log2(1+x0)=log2(
| 1-x0 |
| 1+x0 |
故
| 1-x0 |
| 1+x0 |
| 1 |
| 6 |
解方程得x0=
| 5 |
| 7 |
(3)f(x)=log2(1-x)-log2(1+x),
则f(x)>2等价于
| 1-x |
| 1+x |
解得:-1<x<-
| 3 |
| 5 |
所以x的取值范围是-1<x<-
| 3 |
| 5 |
点评:本题考查的知识点是对数函数的图象与性质的综合应用,函数奇偶性的性质,对数的运算性质,其中根据已知求出函数f(x)的解析式是解答本题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
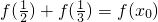 ,求x0的值;
,求x0的值; ,求x的值;
,求x的值;