题目内容
已知函数
的值域为R，则m的取值范围是（ ）A．（-4，+∞）
B．[-4，+∞）
C．（-∞，4）
D．（-∞，-4]
【答案】分析：由题意可得：函数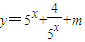
的最小值小于等于0，再由均值不等式可得：
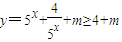，进而得到答案．
解答：解：因为函数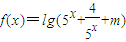
的值域为R，
所以函数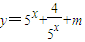
的最小值小于等于0，
由均值不等式可得：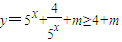
，即
的最小值为：4+m，
所以4+m≤0，即m≤-4．
故选D．
点评：本题值域考查对数函数的性质与值域为全体实数的等价条件的转化，本题是一个易错题，此题也考查了均值不等式的应用，此题属于中档题．
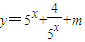的最小值小于等于0，再由均值不等式可得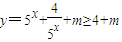：，进而得到答案．解答：解：因为函数
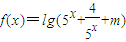的值域为R，所以函数
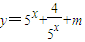的最小值小于等于0，由均值不等式可得：
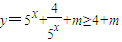，即的最小值为：4+m，所以4+m≤0，即m≤-4．
故选D．
点评：本题值域考查对数函数的性质与值域为全体实数的等价条件的转化，本题是一个易错题，此题也考查了均值不等式的应用，此题属于中档题．
练习册系列答案
相关题目
的值域为R，则m的取值范围为___________________． 
的值域为R，则实数k的取值范围是__________
的值域为R，则实数a的取值范围是 ．
的值域为R，则m的取值范围为（ ）