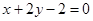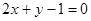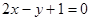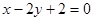题目内容
(本小题满分12分)
设直线
(I)证明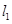 与
与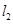 相交;
相交;
(II)证明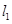 与
与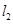 的交点在椭圆
的交点在椭圆
设直线

(I)证明
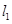 与
与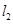 相交;
相交;(II)证明
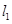 与
与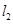 的交点在椭圆
的交点在椭圆
(I)反证法,见解析; (II)交点P在椭圆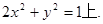
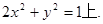
(I)本小题不易直接证明,因而可考虑采用反证法,先假设l1与l2不相交,则l1与l2平行可得k1=k2,这样可以推证与已知条件矛盾.从而问题得证.
(II)先根据l1和l2的方程联立解方程组可求出其交点坐标,然后代入椭圆方程证明方程成立即可.
证明:(I)反证法,假设是l1与l2不相交,则l1与l2平行,有k1=k2,代入k1k2+2=0,得
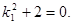 此与k1为实数的事实相矛盾. 从而
此与k1为实数的事实相矛盾. 从而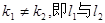 相交. …………5 分
相交. …………5 分
(II)(方法一)由方程组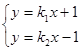 解得交点P的坐标
解得交点P的坐标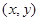 为
为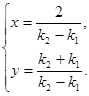
而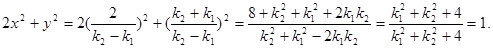
此即表明交点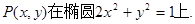 …………12分
…………12分
(方法二)交点P的坐标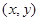 满足
满足
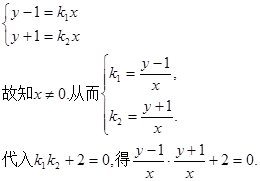
整理后,得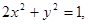 所以交点P在椭圆
所以交点P在椭圆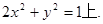
(II)先根据l1和l2的方程联立解方程组可求出其交点坐标,然后代入椭圆方程证明方程成立即可.
证明:(I)反证法,假设是l1与l2不相交,则l1与l2平行,有k1=k2,代入k1k2+2=0,得
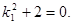 此与k1为实数的事实相矛盾. 从而
此与k1为实数的事实相矛盾. 从而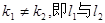 相交. …………5 分
相交. …………5 分(II)(方法一)由方程组
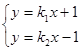 解得交点P的坐标
解得交点P的坐标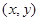 为
为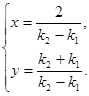
而
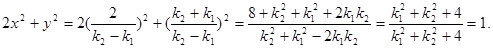
此即表明交点
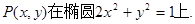 …………12分
…………12分(方法二)交点P的坐标
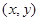 满足
满足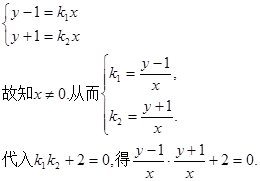
整理后,得
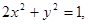 所以交点P在椭圆
所以交点P在椭圆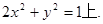

练习册系列答案
 学业测评一课一测系列答案
学业测评一课一测系列答案
相关题目
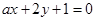 与直线
与直线 互相平行,那么
互相平行,那么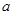 的值等于
的值等于 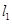 :
: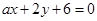 和直线
和直线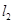 :
: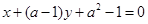 .
.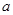 的值.
的值. 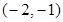 且在两坐标轴上的截距相等,则直线l的方程
且在两坐标轴上的截距相等,则直线l的方程 和
和 轴,
轴,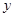 轴分别交于点
轴分别交于点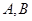 ,以线段
,以线段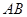 为边在第一象限
为边在第一象限 ,如果在第一象限内有一点
,如果在第一象限内有一点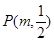 使得△
使得△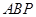 和△
和△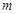 的值。
的值。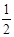 ,-
,-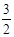 )
)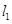 :x-3y+4=0和
:x-3y+4=0和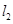 :2x+y+5=0的交点,并且经过原点的直线方程是( )
:2x+y+5=0的交点,并且经过原点的直线方程是( )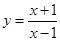 在点
在点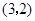 处的切线垂直的直线的方程为( )
处的切线垂直的直线的方程为( )