题目内容
在△ABC中，若（a+b+c）（a+b-c）=3ab，且sinC=2sinAcosB，则△ABC是
- A.等边三角形
- B.等腰三角形但不是等边三角形
- C.等腰直角三角形
- D.直角三角形但不是等腰三角形
A
分析：在△ABC中，由（a+b+c）（a+b-c）=3ab利用余弦定理求得 cosC=
，故 C=60°．再由sinC=2sinAcosB，利用正弦定理、余弦定理可得 a=b，从而判断△ABC的形状．
解答：在△ABC中，∵（a+b+c）（a+b-c）=3ab，∴a2+b2-c2=ab，∴cosC=
=，∴C=60°．
再由 sinC=2sinAcosB，可得 c=2a•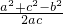
=
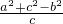，∴a2=b2，∴a=b，
故△ABC是等边三角形，
故选A．
点评：本题主要考查正弦定理和余弦定理的应用，已知三角函数值求角的大小，属于中档题．
分析：在△ABC中，由（a+b+c）（a+b-c）=3ab利用余弦定理求得 cosC=
，故 C=60°．再由sinC=2sinAcosB，利用正弦定理、余弦定理可得 a=b，从而判断△ABC的形状．解答：在△ABC中，∵（a+b+c）（a+b-c）=3ab，∴a2+b2-c2=ab，∴cosC=
=，∴C=60°．再由 sinC=2sinAcosB，可得 c=2a•
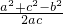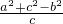=，∴a2=b2，∴a=b，故△ABC是等边三角形，
故选A．
点评：本题主要考查正弦定理和余弦定理的应用，已知三角函数值求角的大小，属于中档题．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
在△ABC中，若
=
，
=
，
=
且
•
=
•
=
•
，则△ABC的形状是△ABC的（ ）
| BC |
| a |
| CA |
| b |
| AB |
| c |
| a |
| b |
| b |
| c |
| c |
| a |
| A、锐角三角形 |
| B、直角三角形 |
| C、等腰直角三角形 |
| D、等边三角形 |
如图，在△ABC中，若在△ABC中，若（a+b+c）（b+c-a）=3bc，且sinA=2sinBcosC，则△ABC的形状是（ ）
| A、直角三角形 | B、等腰直角三角形 | C、等腰三角形 | D、等边三角形 |