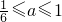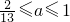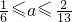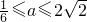题目内容
不等式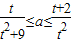
在t∈（0，2]上恒成立，则a的取值范围是（ ）A．
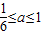
B．
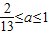
C．
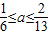
D．
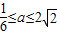
【答案】分析：令f（t）=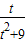
=
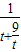，g（t）=
=
=
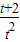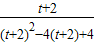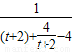，由不等式
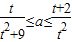在t∈（0，2]上恒成立即f（t）max≤a≤g（t）min，利用函数的单调性可求
解答：解：令f（t）=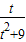
=
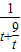，则可得f（t）在t∈（0，2]单调递增，则有f（t）max=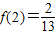
令g（t）=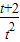
=
=
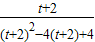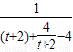在（0，2}单调递减，则有g（t）min=g（2）=1
∵不等式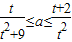
在t∈（0，2]上恒成立
∴f（t）max≤a≤g（t）min
∴
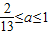
故选：B
点评：本题主要考查了利用函数y=x+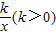
的单调性求解函数的最值，及不等式恒成立与函数最值之间的转化．
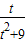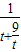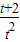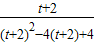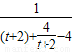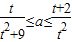=，g（t）===，由不等式在t∈（0，2]上恒成立即f（t）max≤a≤g（t）min，利用函数的单调性可求解答：解：令f（t）=
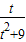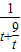=，则可得f（t）在t∈（0，2]单调递增，则有f（t）max=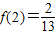令g（t）=
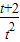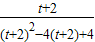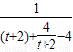==在（0，2}单调递减，则有g（t）min=g（2）=1∵不等式
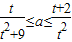在t∈（0，2]上恒成立∴f（t）max≤a≤g（t）min
∴
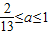
故选：B
点评：本题主要考查了利用函数y=x+
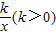的单调性求解函数的最值，及不等式恒成立与函数最值之间的转化． 
练习册系列答案
名校联盟冲刺卷系列答案
名校提分一卷通系列答案
课程达标测试卷闯关100分系列答案
新卷王期末冲刺100分系列答案
相关题目
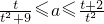在t∈（0，2]上恒成立，则实数a的取值范围是________．
