题目内容
(2013•北京)已知点A(1,-1),B(3,0),C(2,1).若平面区域D由所有满足
=λ
+μ
(1≤λ≤2,0≤μ≤1)的点P组成,则D的面积为
| AP |
| AB |
| AC |
3
3
.分析:设P的坐标为(x,y),根据
=λ
+μ
,结合向量的坐标运算解出
,再由1≤λ≤2、0≤μ≤1得到关于x、y的不等式组,从而得到如图的平行四边形CDEF及其内部,最后根据坐标系内两点间的距离公式即可算出平面区域D的面积.
| AP |
| AB |
| AC |
|
解答:解:设P的坐标为(x,y),则
=(2,1),
=(1,2),
=(x-1,y+1),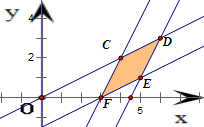
∵
=λ
+μ
,
∴
,解之得
∵1≤λ≤2,0≤μ≤1,∴点P坐标满足不等式组
作出不等式组对应的平面区域,得到如图的平行四边形CDEF及其内部
其中C(4,2),D(6,3),E(5,1),F(3,0)
∵|CF|=
=
,
点E(5,1)到直线CF:2x-y-6=0的距离为d=
=
∴平行四边形CDEF的面积为S=|CF|×d=
×
=3,即动点P构成的平面区域D的面积为3
故答案为:3
| AB |
| AC |
| AP |

∵
| AP |
| AB |
| AC |
∴
|
|
∵1≤λ≤2,0≤μ≤1,∴点P坐标满足不等式组
|
作出不等式组对应的平面区域,得到如图的平行四边形CDEF及其内部
其中C(4,2),D(6,3),E(5,1),F(3,0)
∵|CF|=
| (4-3)2+(2-0)2 |
| 5 |
点E(5,1)到直线CF:2x-y-6=0的距离为d=
| |2×5-1-6| | ||
|
3
| ||
| 5 |
∴平行四边形CDEF的面积为S=|CF|×d=
| 5 |
3
| ||
| 5 |
故答案为:3
点评:本题在平面坐标系内给出向量等式,求满足条件的点P构成的平面区域D的面积.着重考查了平面向量的坐标运算、二元一次不等式组表示的平面区域和点到直线的距离公式等知识,属于中档题.

练习册系列答案
相关题目