题目内容
 如图是某池塘中野生水葫芦的面积与时间的函数关系图象.假设其函数关系为指数函数,并给出下列说法:
如图是某池塘中野生水葫芦的面积与时间的函数关系图象.假设其函数关系为指数函数,并给出下列说法:①此指数函数的底数为2;
②在第5个月时,野生水葫芦的面积会超过30m2;
③野生水葫芦从4m2蔓延到12m2只需1.5个月;
④设野生水葫芦蔓延至2m2、3m2、6m2所需的时间分别为t1、t2、t3则有t1+t2=t3;
其中正确的说法有
①②④
①②④
.(请把正确的说法的序号都填在横线上).分析:根据其关系为指数函数,图象过(4,16)点,得到指数函数的底数为2,当t=5时,s=32>30,利用指对互化做出三个时间的值,结果相等,根据图形的变化趋势得出命题③错误.
解答:解:∵其关系为指数函数,
图象过(4,16)点,
∴指数函数的底数为2,故①正确,
当t=5时,s=32>30,故②正确
4对应的t=2,经过1.5月后面积是23.5<12,故③不正确;
∵t1=1,t2,=log23,t3=log26,
∴有t1+t2=t3,故④正确,
综上可知①②④正确.
故答案为:①②④.
图象过(4,16)点,
∴指数函数的底数为2,故①正确,
当t=5时,s=32>30,故②正确
4对应的t=2,经过1.5月后面积是23.5<12,故③不正确;
∵t1=1,t2,=log23,t3=log26,
∴有t1+t2=t3,故④正确,
综上可知①②④正确.
故答案为:①②④.
点评:本题考查指数函数的变化趋势,解题的关键是题目中有所给的点,根据所给的点做出函数的解析式,从解析式上看出函数的性质.

练习册系列答案
相关题目
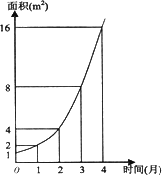

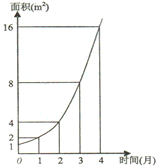 如图是某池塘中野生水葫芦的面积与时间的函数关系图象.假设其函数关系为指数函数,并给出下列说法:
如图是某池塘中野生水葫芦的面积与时间的函数关系图象.假设其函数关系为指数函数,并给出下列说法: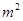 ;
; 、
、 、
、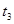 ,则有
,则有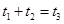 ;
;