题目内容
已知椭圆的方程| x2 |
| 4 |
| y2 |
| 3 |
分析:当△PF1F2内切圆的面积取最大值时即内切圆半径最大即Q点的纵坐标的绝对值最大,因此利用s△ p F1F2 =s△qpF1+s△QF1F2+s△pQ F2可得|y|=
|yp|而|yp|≤
从而可求出Q点的纵坐标的绝对值的最大值,再结合此时p点的特殊位置求横坐标x
| 1 |
| 3 |
| 3 |
解答: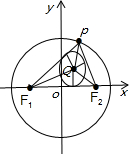 解:如图设内切圆圆心的坐标为Q(x,y)
解:如图设内切圆圆心的坐标为Q(x,y)
∵椭圆的方程
+
=1
∴a2=4,b2=3
∴c2=1,a=2,c=1,pF1+PF2=2a=4,F1F2=2C=2
又∵s△ p F1F2 =s△qpF1+s△QF1F2+s△pQ F2
∴
×F1F2×|yp|=
×(pF1+pF2+F1F2)×|y|
∴|y|=
|yp|..
又∵|yp|≤
∴|y|≤
此时p点在椭圆与y轴相交的两个顶点上故x=0同时内切圆面积为πy2≤
∴Q(
,0)
故答案为(
,0)
 解:如图设内切圆圆心的坐标为Q(x,y)
解:如图设内切圆圆心的坐标为Q(x,y)∵椭圆的方程
| x2 |
| 4 |
| y2 |
| 3 |
∴a2=4,b2=3
∴c2=1,a=2,c=1,pF1+PF2=2a=4,F1F2=2C=2
又∵s△ p F1F2 =s△qpF1+s△QF1F2+s△pQ F2
∴
| 1 |
| 2 |
| 1 |
| 2 |
∴|y|=
| 1 |
| 3 |
又∵|yp|≤
| 3 |
∴|y|≤
| ||
| 3 |
| π |
| 3 |
∴Q(
| + |
. |
| ||
| 3 |
故答案为(
| + |
. |
| ||
| 3 |
点评:此题主要考查了椭圆与圆的综合问题.关键是要分析出△PF1F2内切圆的面积取最大值时即内切圆半径最大即Q点的纵坐标的绝对值最大同时还要利用面积分割得到关系式|y|=
|yp|再利用|yp|≤
求得Q点的纵坐标的绝对值的最大值.此题另一关键是要得出当内切圆面积最大时p点落在椭圆与Y轴的交点上此时x=0.此题充分体现了数形结合思想在解题中得应用!
| 1 |
| 3 |
| 3 |

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
已知实系数方程x2+(a+1)x+a+b+1=0的两根分别为一个椭圆和一个双曲线的离心率,则
的取值范围是( )
| b |
| a |
| A、(-2,-1) | ||
B、(-1,-
| ||
C、(-2,-
| ||
| D、(-2,+∞) |
 如图,已知椭圆E1方程为
如图,已知椭圆E1方程为