题目内容
已知抛物线的顶点在原点,焦点在y轴上,其上的点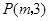 到焦点的距离为5,则抛物线方程为( )
到焦点的距离为5,则抛物线方程为( )
A.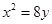 B.
B.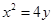
C.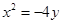 D.
D.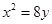
【答案】
A
【解析】
试题分析:∵抛物线的顶点在原点,焦点在y轴上,抛物线上一点(m, 3),
∴设抛物线的方程为:x2=2py(p>0),
∴其准线方程为:y=-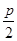 ,
,
∵抛物线上一点P(m, 3)到焦点F的距离等于5,
∴由抛物线的定义得:|PF|= 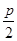 +3=5,∴p=4,
+3=5,∴p=4,
∴所求抛物线的方程为x2=8y.故选A。
考点:本题主要考查抛物线的定义、标准方程及几何性质。
点评:求抛物线标准方程,首先应根据开口方向、焦点位置,确定方程形式。

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目